優選學

優選學中的一些理論和方法首先被應用於化工與電子行業中工藝參數的優選、儀器設備的調試控制等方面，然後逐步在石油、冶金、煤炭、建材、紡織、糧食加工、機械、醫療衛生等領域得到了開發和應用。70年代中期以來，優選與電子計算機相結合，在優化設計、新產品試製、模型參數的識別、經濟決策、經濟發展規劃優選等方面取得了很好的效果和經驗。

為了推廣優選方法，中國數學家華羅庚在理論研究和開發研究工作的基礎上，選定了幾種理論上靠得住、又易於應用的方法，編寫出《優選法平話》（署名齊念一，1971）和《優選法平話及其補充》(1971)等通俗小冊子。他帶領優選法推廣小分隊到國內大部分省、市、自治區，向生產單位介紹方法和應用案例，組織推廣和應用。人們應用這些方法，取得了大量的優選法成果，在不增加投資、設備和人力的條件下，為實現優質、高產、低消耗，取得了明顯的經濟效益和社會效益。有些成果已編入《全國優選法成果彙編》(1977)等文集中。優選法幾次被定為國內重點推廣項目，並被國家經濟委員會評為在國內應用範圍廣泛、效果明顯的方法之一。

一般的優選問題常可在數學上表達為在一定條件下求取最優解，即：

[805-1]式中為決策變數，()為目標函數,()≥0和()=0分別為不等式約束和等式約束。

決策變數可以是單變數，也可以是向量：=(,,…，)。當≥2時稱為多變數優選問題。若是時間的函數 =()，則稱為動態優選問題。當是隨機變數時，稱為隨機優選問題。若目標函數()是向量函數：

[805-2]),稱為多目標優選問題。同樣,()和()可看作是的向量函數。當約束條件不存在時，稱為無約束優化問題。

①

目標函數或約束條件不能用明顯的數學表達式表示，或有數學表達式能計算出每點的函數值，但()的導數不存在。此時只能通過實驗(或計算)獲得目標函數值。問題在於如何利用儘可能少的試驗次數，儘快地找到最優解。選擇最佳工藝條件和最佳配方、設備儀器調試等問題便屬於這一類。這一類的優選方法有:0.618法(黃金分割法)；對分法；一批作多個試驗的方法；分數法；拋物線法；因素輪換法；從好點出發法；各類爬山法；陡度法；平行線法；切塊法；拋物體法，等等。

②

目標函數與約束條件均可用明顯數學表達式表示。最簡單的數學表達式是線性函數，此時可用線性規劃的方法去求解。在一般情況，上述函數中的全部或一部分常常是非線性的，所對應的求解方法是非線性優化，或稱非線性優選法。例如二次規劃，最小二乘法，梯度法，牛頓類的方法，以及在第一類模型中所用的一些方法，等等。

③

決策變數是某函數族中的元素。此時的優選模型是在一定的約束條件下求函數族中的最優函數。例如當決策變數和時間有關，即=()時的動態優化或多階段優化模型，屬於這一類。求解這類模型，除了在第一、二類模型中所用的方法外，還有變分法、動態規劃、最大值原理和控制理論中的一些方法。

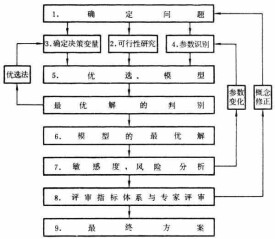
對於實際問題的優選過程可用如右上圖表示。

①確定問題　首先對優選問題作目標分析，即優選的目的是什麼？達到這目的的手段以及影響此目的的因素有哪些？這些手段和因素受哪些條件的制約？以上有關的目的、手段、因素、條件中哪些是定性的？哪些是定量的？然後明確所要解決的問題的邊界、本問題與外界的聯繫、決策方案的含義、決策的目標、方案效果的評價標準。

②方案可行性條件的研究　確定可供選擇的方案集合以及這些方案的限制條件。例如在工藝優選實驗中，實驗範圍內部與外部的技術、經濟、社會、資源等條件的限制。

③ 確定決策變數 決定用哪些變數或函數來描述決策方案。例如在無線電網路優化設計中，決策變數為電子元件的電阻、電容、電感的數值等。

④ 模型參數識別　優選模型中，除決策變數和控制變數外的其他參數稱為模型參數，這些參數在模型中為給定的已知數，但在實際問題中往往還需要通過某些途徑來確定。例如，反映外界條件限制的市場需要量要根據市場預測來決定；計劃模型中的人、財、物的消耗定額，需要進行定額分析來給出，等等。

⑤ 確定優選模型 這一步是通過對目標函數及約束條件的分析以建立優選的數學模型。目標函數的分析是將決策目標分為能用數量描述的定量指標和不能用數量描述的定性指標，分析判斷需要納入優選數學模型的目標，其中哪些目標作為模型的目標函數；哪些目標將轉換成約束條件並用控制變數進行控制（例如將投資均衡換成約束條件，用上下波動幅度來控制）；約束條件的分析是確定納入模型的可行性限制條件能否用決策變數和控制變數之間的函數關係表示，若能夠，則寫出約束條件方程。未列入目標函數或約束條件的那些評價標準和可行性限制條件可留作方案最終評審的依據。

⑥ 求解數學模型　根據優選數學模型的特點，用相應的優選方法尋找出最優解。有時由於尋找最優解的代價太大，而實際情況又允許，只需尋找滿意的近似最優解或合理解。

⑦ 敏感度與風險分析 建立敏感度分析的有關模型，研究由於控制變數或模型參數的變化對最終方案的指標和合理性可能產生的影響，用以評價優選方案的穩定性和決策方案所冒的風險。

⑧ 優選方案評審 由決策者組織各方面有關的專家，對優選數學模型輸出的優選方案進行評審。仔細考察相應於優選方案的評價指標和敏感度分析的結果是否滿足實際需要；未列入模型的其他評價標準和可行性限制條件是否得到滿足；還可以同經驗方案進行對比以決定優劣。經過評審，往往需要對模型的概念作修改，即修改決策變數或模型中的目標函數和約束條件，也可能需要改變對模型參數的控制，然後重複③至⑧各步驟。

⑨ 確定最終優選方案 評審通過的方案投入實際使用，經實踐檢驗滿意的方案便被確定為最終優選方案，否則還需進一步修改完善，重複上述的步驟。

從上述優選過程可以看出，在尋求管理或技術等領域中的最優方案時，用數學方法求出優選數學模型的最優解只是此過程的一個重要組成部分，但不是全部。優選過程還包括了在此以前的對實際問題的研究和目標分析、建立優選數學模型、模型和參數的識別、在求出數學模型最優解后的敏感度分析、對最優的（或近似最優的）決策方案的評審、以及信息的反饋等。