第一象限
平面直角坐標系中右上角的象限
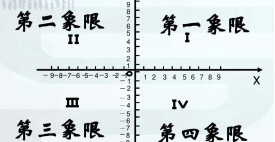
象限,又稱象限角(英文:Quadrant意思是一圓之四分一等份),是直角坐標系(笛卡爾坐標系)中,主要應用於三角學和複數的阿根圖(複平面)中的坐標系。平面直角坐標系裡的橫軸和縱軸所劃分的四個區域,分為四個象限。象限以原點為中心,x,y軸為分界線。右上的稱為第一象限,左上的稱為第二象限,左下的稱為第三象限,右下的稱為第四象限。坐標軸上的點不屬於任何象限。
在應用數學里,平面直角坐標系中,右上角的象限稱為第一象限。
第一象限
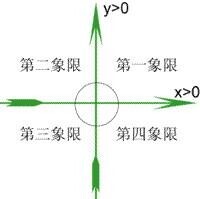
在數軸上0點處再加一條垂直直線,就成了一個笛卡兒坐標圖,右上角那一塊區域稱為第一象限,上面左邊那一塊為第二象限,第二象限的下面為第三象限,然後第一象限的下面,即第三象限的右邊稱做第四象限.
這時角的概念就是x軸正方向那條射線(右邊那條),繞O點逆時針轉過的角度。可以繞很多圈,比如繞了2圈又回到x軸正方向,那這個角就為720度。
第一象限角:(正+,+正),橫縱坐標同號,記作。
只要這條射線最終落在第一象限,(不包括x,y軸),就稱為第一象限角,有我們通常熟悉的0-90度,還有360-450 ,720-810等,
在第一象限的角的sin值,cos值,tan值均為正數。
可以看該角的終邊上的任意一點的坐標(x,y)
時在第一象限
時在第二象限
時在第三象限
時在第四象限
也可以根據角度來看,設角度為α時,在第一象限
時,在第二象限
時,在第三象限
時,在第四象限
為任意整數,另外這裡我用的是弧度制,度
第一象限:(正+,+正),橫縱坐標同號,記作
第二象限:(負-,+正),橫縱坐標異號,記作
第三象限:(負-,-負),橫縱坐標同號,記作
第四象限:(正+,-負),橫縱坐標異號,記作
x軸正方向:(+,0)
x軸負方向:(-,0)
y軸正方向:(0,+)
y軸負方向:(0,-)
*註:在坐標軸上的點,不在象限內。