哈希表
根據關鍵碼值而直接進行訪問的數據結構
散列表(Hash table,也叫哈希表),是根據關鍵碼值(Key value)而直接進行訪問的數據結構。也就是說,它通過把關鍵碼值映射到表中一個位置來訪問記錄,以加快查找的速度。這個映射函數叫做散列函數,存放記錄的數組叫做散列表。
給定表M,存在函數f(key),對任意給定的關鍵字值key,代入函數后若能得到包含該關鍵字的記錄在表中的地址,則稱表M為哈希(Hash)表,函數f(key)為哈希(Hash) 函數。
● 若關鍵字為k,則其值存放在f(k)的存儲位置上。由此,不需比較便可直接取得所查記錄。稱這個對應關係f為散列函數,按這個思想建立的表為散列表。
● 對不同的關鍵字可能得到同一散列地址,即k1≠k2,而f(k1)=f(k2),這種現象稱為衝突(英語:Collision)。具有相同函數值的關鍵字對該散列函數來說稱做同義詞。綜上所述,根據散列函數f(k)和處理衝突的方法將一組關鍵字映射到一個有限的連續的地址集(區間)上,並以關鍵字在地址集中的“像”作為記錄在表中的存儲位置,這種表便稱為散列表,這一映射過程稱為散列造表或散列,所得的存儲位置稱散列地址。
● 若對於關鍵字集合中的任一個關鍵字,經散列函數映象到地址集合中任何一個地址的概率是相等的,則稱此類散列函數為均勻散列函數(Uniform Hash function),這就是使關鍵字經過散列函數得到一個“隨機的地址”,從而減少衝突。
1. 開放定址法:Hi=(H(key) + di) MOD m,i=1,2,…,k(k<=m-1),其中H(key)為散列函數,m為散列表長,di為增量序列,可有下列三種取法:
1.1. di=1,2,3,…,m-1,稱線性探測再散列。
1.2. di=1^2,-1^2,2^2,-2^2,⑶^2,…,±(k)^2,(k<=m/2)稱二次探測再散列。
1.3. di=偽隨機數序列,稱偽隨機探測再散列。
2. 再散列法:Hi=RHi(key),i=1,2,…,k RHi均是不同的散列函數,即在同義詞產生地址衝突時計算另一個散列函數地址,直到衝突不再發生,這種方法不易產生“聚集”,但增加了計算時間。
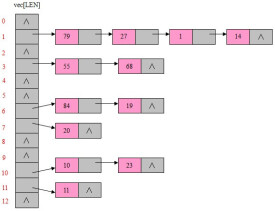
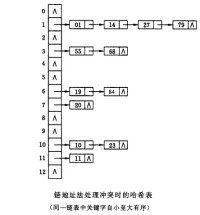
3. 鏈地址法(拉鏈法)。
4. 建立一個公共溢出區。
散列函數能使對一個數據序列的訪問過程更加迅速有效,通過散列函數,數據元素將被更快地定位。
實際工作中需視不同的情況採用不同的哈希函數,通常考慮的因素有:
· 計算哈希函數所需時間
· 關鍵字的長度
· 哈希表的大小
· 關鍵字的分佈情況
· 記錄的查找頻率
1. 直接定址法:取關鍵字或關鍵字的某個線性函數值為散列地址。即H(key)=key或H(key) = a·key + b,其中a和b為常數(這種散列函數叫做自身函數)。若其中H(key)中已經有值了,就往下一個找,直到H(key)中沒有值了,就放進去。
2. 數字分析法:分析一組數據,比如一組員工的出生年月日,這時我們發現出生年月日的前幾位數字大體相同,這樣的話,出現衝突的幾率就會很大,但是我們發現年月日的後幾位表示月份和具體日期的數字差別很大,如果用後面的數字來構成散列地址,則衝突的幾率會明顯降低。因此數字分析法就是找出數字的規律,儘可能利用這些數據來構造衝突幾率較低的散列地址。
3. 平方取中法:當無法確定關鍵字中哪幾位分佈較均勻時,可以先求出關鍵字的平方值,然後按需要取平方值的中間幾位作為哈希地址。這是因為:平方后中間幾位和關鍵字中每一位都相關,故不同關鍵字會以較高的概率產生不同的哈希地址。
例:我們把英文字母在字母表中的位置序號作為該英文字母的內部編碼。例如K的內部編碼為11,E的內部編碼為05,Y的內部編碼為25,A的內部編碼為01, B的內部編碼為02。由此組成關鍵字“KEYA”的內部代碼為11052501,同理我們可以得到關鍵字“KYAB”、“AKEY”、“BKEY”的內部編碼。之後對關鍵字進行平方運算后,取出第7到第9位作為該關鍵字哈希地址,如下圖所示
| 關鍵字 | 內部編碼 | 內部編碼的平方值 | H(k)關鍵字的哈希地址 |
| KEYA | 11050201 | 122157778355001 | 778 |
| KYAB | 11250102 | 126564795010404 | 795 |
| AKEY | 01110525 | 001233265775625 | 265 |
| BKEY | 02110525 | 004454315775625 | 315 |
4. 摺疊法:將關鍵字分割成位數相同的幾部分,最後一部分位數可以不同,然後取這幾部分的疊加和(去除進位)作為散列地址。數位疊加可以有移位疊加和間界疊加兩種方法。移位疊加是將分割后的每一部分的最低位對齊,然後相加;間界疊加是從一端向另一端沿分割界來回摺疊,然後對齊相加。
5. 隨機數法:選擇一隨機函數,取關鍵字的隨機值作為散列地址,通常用於關鍵字長度不同的場合。
6. 除留餘數法:取關鍵字被某個不大於散列表表長m的數p除后所得的餘數為散列地址。即 H(key) = key MOD p,p<=m。不僅可以對關鍵字直接取模,也可在摺疊、平方取中等運算之後取模。對p的選擇很重要,一般取素數或m,若p選得不好,容易產生同義詞。
散列表的查找過程基本上和造表過程相同。一些關鍵碼可通過散列函數轉換的地址直接找到,另一些關鍵碼在散列函數得到的地址上產生了衝突,需要按處理衝突的方法進行查找。在介紹的三種處理衝突的方法中,產生衝突后的查找仍然是給定值與關鍵碼進行比較的過程。所以,對散列表查找效率的量度,依然用平均查找長度來衡量。
查找過程中,關鍵碼的比較次數,取決於產生衝突的多少,產生的衝突少,查找效率就高,產生的衝突多,查找效率就低。因此,影響產生衝突多少的因素,也就是影響查找效率的因素。影響產生衝突多少有以下三個因素:
1. 散列函數是否均勻;
2. 處理衝突的方法;
3. 散列表的裝填因子。
散列表的裝填因子定義為:α= 填入表中的元素個數 / 散列表的長度
α是散列表裝滿程度的標誌因子。由於表長是定值,α與“填入表中的元素個數”成正比,所以,α越大,填入表中的元素較多,產生衝突的可能性就越大;α越小,填入表中的元素較少,產生衝突的可能性就越小。
實際上,散列表的平均查找長度是裝填因子α的函數,只是不同處理衝突的方法有不同的函數。
了解了hash基本定義,就不能不提到一些著名的hash演演算法,MD5 和 SHA-1 可以說是目前應用最廣泛的Hash演演算法,而它們都是以 MD4 為基礎設計的。那麼他們都是什麼意思呢?
這裡簡單說一下:
⑴ MD4
MD4(RFC 1320)是 MIT 的 Ronald L. Rivest 在 1990 年設計的,MD 是 Message Digest 的縮寫。它適用在32位字長的處理器上用高速軟體實現--它是基於 32 位操作數的位操作來實現的。
哈希表
MD5(RFC 1321)是 Rivest 於1991年對MD4的改進版本。它對輸入仍以512位分組,其輸出是4個32位字的級聯,與 MD4 相同。MD5比MD4來得複雜,並且速度較之要慢一點,但更安全,在抗分析和抗差分方面表現更好
⑶ SHA-1 及其他
SHA1是由NIST NSA設計為同DSA一起使用的,它對長度小於264的輸入,產生長度為160bit的散列值,因此抗窮舉(brute-force)性更好。SHA-1 設計師基於和MD4相同原理,並且模仿了該演演算法。
那麼這些Hash演演算法到底有什麼用呢?
Hash演演算法在信息安全方面的應用主要體現在以下的3個方面:
⑴ 文件校驗
比較熟悉的校驗演演算法有奇偶校驗和CRC校驗,這2種校驗並沒有抗數據篡改的能力,它們一定程度上能檢測出數據傳輸中的通道誤碼,但卻不能防止對數據的惡意破壞。
MD5 Hash演演算法的"數字指紋"特性,使它成為目前應用最廣泛的一種文件完整性校驗和(Checksum)演演算法,不少Unix系統有提供計算md5 checksum的命令。
⑵ 數字簽名
Hash 演演算法也是現代密碼體系中的一個重要組成部分。由於非對稱演演算法的運算速度較慢,所以在數字簽名協議中,單向散列函數扮演了一個重要的角色。對 Hash 值,又稱"數字摘要"進行數字簽名,在統計上可以認為與對文件本身進行數字簽名是等效的。而且這樣的協議還有其他的優點。
⑶ 鑒權協議
如下的鑒權協議又被稱作挑戰--認證模式:在傳輸通道是可被偵聽,但不可被篡改的情況下,這是一種簡單而安全的方法。
MD5、SHA1的破解
2004年8月17日,在美國加州聖芭芭拉召開的國際密碼大會上,山東大學王小雲教授在國際會議上首次宣布了她及她的研究小組近年來的研究成果——對MD5、HAVAL-128、MD4和RIPEMD等四個著名密碼演演算法的破譯結果。次年二月宣布破解SHA-1密碼。
以上就是一些關於hash以及其相關的一些基本預備知識。那麼在emule裡面他具體起到什麼作用呢?
大家都知道emule是基於P2P (Peer-to-peer的縮寫,指的是點對點的意思的軟體),它採用了"多源文件傳輸協議”(MFTP,the Multisource FileTransfer Protocol)。在協議中,定義了一系列傳輸、壓縮和打包還有積分的標準,emule 對於每個文件都有md5-hash的演演算法設置,這使得該文件獨一無二,並且在整個網路上都可以追蹤得到。
什麼是文件的hash值呢?
MD5-Hash-文件的數字文件通過Hash函數計算得到。不管文件長度如何,它的Hash函數計算結果是一個固定長度的數字。與加密演演算法不同,這一個Hash演演算法是一個不可逆的單向函數。採用安全性高的Hash演演算法,如MD5、SHA時,兩個不同的文件幾乎不可能得到相同的Hash結果。因此,一旦文件被修改,就可檢測出來。
當文件放到emule裡面進行共享發布的時候,emule會根據hash演演算法自動生成這個文件的hash值,他就是這個文件唯一的身份標誌,它包含了這個文件的基本信息,然後把它提交到所連接的伺服器。當有他人想對這個文件提出下載請求的時候,這個hash值可以讓他人知道他正在下載的文件是不是就是他所想要的。尤其是在文件的其他屬性被更改之後(如名稱等)這個值就更顯得重要。而且伺服器還提供了,這個文件當前所在的用戶的地址,埠等信息,這樣emule就知道到哪裡去下載了。
哈希表
對於emule中文件的hash值是固定的,也是唯一的,它就相當於這個文件的信息摘要,無論這個文件在誰的機器上,他的hash值都是不變的,無論過了多長時間,這個值始終如一,當在進行文件的下載上傳過程中,emule都是通過這個值來確定文件。
那麼什麼是userhash呢?
道理同上,當在第一次使用emule的時候,emule會自動生成一個值,這個值也是唯一的,它是在emule世界裡面的標誌,只要你不卸載,不刪除config,你的userhash值也就永遠不變,積分制度就是通過這個值在起作用,emule裡面的積分保存,身份識別,都是使用這個值,而和你的id和你的用戶名無關,你隨便怎麼改這些東西,你的userhash值都是不變的,這也充分保證了公平性。其實他也是一個信息摘要,只不過保存的不是文件信息,而是每個人的信息。
那麼什麼是hash文件呢?
經常在emule日誌裡面看到,emule正在hash文件,這裡就是利用了hash演演算法的文件校驗性這個功能了,文章前面已經說了一些這些功能,其實這部分是一個非常複雜的過程,目前在ftp,bt等軟體裡面都是用的這個基本原理,emule裡面是採用文件分塊傳輸,這樣傳輸的每一塊都要進行對比校驗,如果錯誤則要進行重新下載,這期間這些相關信息寫入met文件,直到整個任務完成,這個時候part文件進行重新命名,然後使用move命令,把它傳送到incoming文件裡面,然後met文件自動刪除,所以有的時候會遇到hash文件失敗,就是指的是met裡面的信息出了錯誤不能夠和part文件匹配,另外有的時候開機也要瘋狂hash,有兩種情況一種是你在第一次使用,這個時候要hash提取所有文件信息,還有一種情況就是上一次你非法關機,那麼這個時候就是要進行排錯校驗了。
關於hash的演演算法研究,一直是信息科學裡面的一個前沿,尤其在網路技術普及的今天,他的重要性越來越突出,其實每天在網上進行的信息交流安全驗證,在使用的操作系統密鑰原理,裡面都有它的身影,特別對於那些研究信息安全有興趣的朋友,這更是一個打開信息世界的鑰匙,他在hack世界裡面也是一個研究的焦點。
一般的線性表、樹中,記錄在結構中的相對位置是隨機的即和記錄的關鍵字之間不存在確定的關係,在結構中查找記錄時需進行一系列和關鍵字的比較。這一類查找方法建立在“比較”的基礎上,查找的效率與比較次數密切相關。理想的情況是能直接找到需要的記錄,因此必須在記錄的存儲位置和它的關鍵字之間建立一確定的對應關係f,使每個關鍵字和結構中一個唯一的存儲位置相對應。因而查找時,只需根據這個對應關係f找到給定值K得像f(K)。若結構中存在關鍵字和K相等的記錄,則必定在f(K)的存儲位置上,由此不需要進行比較便可直接取得所查記錄。在此,稱這個對應關係f為哈希函數,按這個思想建立的表為哈希表(又稱為雜湊法或散列表)。
哈希表不可避免衝突(collision)現象:對不同的關鍵字可能得到同一哈希地址 即key1≠key2,而hash(key1)=hash(key2)。具有相同函數值的關鍵字對該哈希函數來說稱為同義詞(synonym)。因此,在建造哈希表時不僅要設定一個好的哈希函數,而且還要設定一種處理衝突的方法。可如下描述哈希表:根據設定的哈希函數H(key)和所選中的處理衝突的方法,將一組關鍵字映象到一個有限的、地址連續的地址集(區間)上並以關鍵字在地址集中的“象”作為相應記錄在表中的存儲位置,這種表被稱為哈希表。
對於動態查找表而言,1) 表長不確定;2)在設計查找表時,只知道關鍵字所屬範圍,而不知道確切的關鍵字。因此,一般情況需建立一個函數關係,以f(key)作為關鍵字為key的錄在表中的位置,通常稱這個函數f(key)為哈希函數。(注意:這個函數並不一定是數學函數)
哈希函數是一個映象,即:將關鍵字的集合映射到某個地址集合上,它的設置很靈活,只要這個地址集合的大小不超出允許範圍即可。
現實中哈希函數是需要構造的,並且構造的好才能使用的好。
用途:加密,解決衝突問題。
用途很廣,比特精靈中就使用了哈希函數,你可以自己看看。
具體可以學習一下數據結構和演演算法的書。
哈希表
int ELFhash(char *key)
{
unsigned long h=0;
while(*key)
{
h=(h<<4)+*key++;
unsigned long g=h&0Xf0000000L;
if(g)
h^=g>>24;
h&=~g;
}
return h%MOD;
}