CRC
循環冗餘校驗
循環冗餘校驗(Cyclic Redundancy Check, CRC)是一種根據網路數據包或電腦文件等數據產生簡短固定位數校驗碼的一種散列函數,主要用來檢測或校驗數據傳輸或者保存后可能出現的錯誤。它是利用除法及餘數的原理來作錯誤偵測的。
在數據傳輸過程中,無論傳輸系統的設計再怎麼完美,差錯總會存在,這種差錯可能會導致在鏈路上傳輸的一個或者多個幀被破壞(出現比特差錯,0變為1,或者1變為0),從而接受方接收到錯誤的數據。為盡量提高接受方收到數據的正確率,在接收方接收數據之前需要對數據進行差錯檢測,當且僅當檢測的結果為正確時接收方才真正收下數據。檢測的方式有多種,常見的有奇偶校驗、網際網路校驗和循環冗餘校驗等。
循環冗餘校驗同其他差錯檢測方式一樣,通過在要傳輸的k比特數據D后添加(n-k)比特冗餘位(又稱幀檢驗序列,Frame Check Sequence,FCS)F形成n比特的傳輸幀T,再將其發送出去。
校驗碼格式
T mod P == 0 ……(1)
其中 T =2D + F
基於上述要求,實際應用時,發送方和接收方按以下方式通信:
1. 發送方和接收方在通信前,約定好預設整數P。
2. 發送方在發送前根據數據D確定滿足(1)式的F,生成CRC碼 T,T 即為數據位D與校驗位F的拼接,發送T。
3. 接收方收到CRC碼 T,進行 result = T mod P 運算,當且僅當result = 0時接收方認為沒有差錯。
發送方在發送數據前需要確定填充的(n-k)比特F,以下提供了兩種等價的方式來確定F。
模二運算
模二運算採用無進位的二進位加法,恰好為異或(XOR)操作。(以下運算均為模2運算)
CRC碼 T 需要滿足(1)式,即 (2D + F)/P結果為某一整數
對此表達式進行恆等變換,可得:
(2D + F)/P = 2D / P + F / P …… (2)
繼續對等式中 2D / P 進行恆等變換,將其整數部分 Q 分離,即 Q=(2D - R)/P,有
2D / P = Q + R / P …… (3)
將(3)式帶入(2)式 得到:
(2D + F) / P = Q + R / P+ F / P …… (4)
由於採用無進位的二進位加法(等價於XOR操作),因此當我們令 F = R 時,有
(2D + F) / P = Q + R / P+ F / P = Q …… (5)
當Q為整數時, T =(2D + F)滿足 T mod P == 0。
故我們只要找到 F = R 使得(3)式中 Q 恆為整數即可。
由 Q=(2D - R)/P,可知
(1)當 2D modP ≠ 0 時
R=2D modP可使等式恆成立。
(2)當 2D modP == 0 時
F = R = n * P(n ∈ Z)可使等式恆成立。
R=2D modP 即為 n = 0 時情況。
綜上,令 R=2D modP 時 可使等式 Q=(2D - R)/P 中Q恆為整數。
因此我們需要添加的幀檢驗序列F為:
F = R=2D modP …… (6)
二進位係數多項式
該種方法,我們試圖對任意的二進位數都構造與其對應的一個二進位係數多項式,構造如下:
對於任意k位二進位數D =d…ddd,其對應的多項式為
D(X) = ∑d*X,i∊[0, k) …… (7)
例如,D = 110101,則D(X) = X + X + X + 1。
運算過程依然是模二的,則此時的CRC過程可描述如下:
XD(X) / P(X) = Q(X) + R(X) / P(X) …… (8)
T(X) = XD(X) + R(X) …… (9)
即,此時的F(X)滿足:
F(X) = XD(X) mod P(X) …… (10)
上面我們介紹了F(X)的求法,但F(X)依賴於P(X),因此選取一個合適的P(X)也是CRC的一個關鍵問題。通常,一個m位的CRC多項式P(X)是由如下兩種形式的多項式之一產生的:
P(X) = q(X) …… (12)
P(X) = (X + 1)q(X) …… (13)
其中q(X)是一種特殊類型的多項式,稱為本原多項式。且P(X)滿足:
• 最高位和最低位都是1
• 當被傳送信息任何一位發生錯誤時,P(X)不被T(X)整除
• 不同位發生錯誤時,餘數應該不同
• 對餘數繼續做模二除法時,應該使餘數循環
下面展示常用CRC版本:
| 名稱 | 多項式 | 表示法 | 應用舉例 |
| CRC-8 | X+X+X+1 | 0X207 | |
| CRC-12 | X+X+X+X+X+1 | 0X80F | telecom systems |
| CRC-16 | X+X+X+1 | 0X8005 | Bisync, Modbus, USB, ANSI X3.28, SIA DC-07, many others; also known as CRC-16 and CRC-16-ANSI |
| CRC-CCITT | X+X+X+1 | 0X1021 | ISO HDLC, ITU X.25, V.34/V.41/V.42, PPP-FCS |
| CRC-32 | X+X+X+X+X+X+X+X+X+X+X+X+X+X+1 | 0x04C11DB7 | ZIP, RAR, IEEE 802 LAN/FDDI, IEEE 1394, PPP-FCS |
| CRC-32C | X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+1 | 0x1EDC6F41 | iSCSI, SCTP, G.hn payload, SSE4.2, Btrfs, ext4, Ceph |
上面我們提供了很多國際標準的CRC生成多項式版本,但在我們實際的應用當中,我們只需要選擇其中的一種作為生成多項式即可,可是我們應該如何做出選擇呢?下面我們根據幾張8bits-16bits實驗模擬圖來對不同的標準進行橫向和豎向的比較,從而給出一種比較合適的選擇方案。
註:
1. 以下幾圖中,藍色虛線為實驗者提出的標準最小漏檢率曲線,下面我們稱為最佳性能曲線。
2. 以下圖和數據來自《CRC性能分析及生成多項式選取的研究》,碩士學位論文,鄭州輕工業學院魏艷。

8bits-16bits性能圖
8-bits CRC
 8bits-1 | 左圖1中,0xD5為CRC-8標準,從以上兩圖中我們可以看到: 1. 該標準對於8bits-85bits的範圍內表現出了優良的性能,貼近最佳性能曲線;當數據幀的長度長於85bits的時候其性能出現了驟變,漏檢率提高,性能下降;當數據幀長度達到248bits的時候,性能略微回歸,但仍然表現不佳。 2. 相比較CRC-8標準而言,生成多項式0x2F表現出了更好的性能,但仍舊在128bits-256bits區間表現不佳。 3. 從左圖2二可見,生成多項式0x4D彌補了上述兩個生成多項式在128bits-后表現不佳的缺點。 |
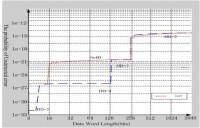 8bits-2 | 因此,我們可以得出結論,若CRC長度限制在8bits,我們根據所給數據幀的最小長度來確定合適的CRC多項式: 8bits-85bits:選擇CRC-8標準,漏檢率大概在(1e-27, 1e-24) 8bits-128bits:選擇0x2F,漏檢率大概在(1e-27, 1e-24) 128bits-2048bits:選擇0x4D,漏檢率大概在(1e-21, 1e-12) |
12-bits CRC
 12bits | 在12bits下,國際上有CRC-12標準0x80F,我們仍然以橫向比較來進行。上圖告訴我們: 1. CRC-12標準整體表現不盡如人意,在實驗者選取的數據幀長度(我們常用的數據幀長度範圍)內,CRC-12標準的漏檢率整體高於最佳性能曲線。 2. 就該標準而言,在54bits-2035bits範圍內表現較好。 因此我們可以得出結論,若CRC長度限制在12bits,可以選擇CRC-12標準,但更傾向於數據幀長度在54bits-2035bits範圍內。 |
16-bits CRC
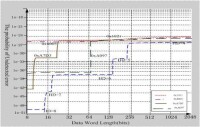 16bits | 同樣利用實驗者的數據,我們對16-bits的國際標準美國標準CRC-16(0x8005)和歐洲標準CRC-CCITT(0x1021)進行比較: 1. 在漏檢率方面,歐洲標準略低於美國標準。 2. 上述兩種標準的生成多項式性能表現不是很理想,在8bits-247bits範圍內校驗性能較差。 由此,我們得出: 16-bits的美國標準和歐洲標準更適合於長度大於256bits的幀。 |
二、縱向比較
上面,我們利用實驗者提供的實驗數據對限長的CRC國際標準碼的性能表現做了橫向比較,下面我們進行部分縱向比較,僅考慮數據幀長度,而不限制CRC長度。
從實驗者提供的數據我們可以發現,對於國際標準CRC-8,CRC-12,CRC-16,CRC-CCITT:
1. 當數據幀長度在8bits-128bits範圍內時,CRC-8有更好的表現;
2. 當數據幀長度大於128bits時,CRC-12,CRC-16,CRC-CCITT均有較好的表現,且其漏檢率基本相近。
三、結論
基於上述簡單的分析,以及更多的實驗,實驗者給出了選擇CRC生成多項式的具體步驟,並提供了一張對應於不同長度數據幀的相對比較好的CRC生成多項式的選擇表。
| 生成多項式最小碼距 | CRC Size(bits) | |||||||||||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| HD=2 | 2048+ 0X5 | 2048+ 0X9 | 2048+ 0X12 | 2048+ 0X21 | 2048+ 0X48 | 2048+ 0x4D | 2048+ 0X2CF | 2048+ 0x64F | 2048+ 0X64D | |||||
| HD=3 | 11 0X9 | 26 0X12 | 57 0X21 | 120 0X48 | 247 0X4D | 502 0X2CF | 1013 0X64F | 2036 0X64D | 2048 0x6EB | |||||
| HD=4 | 10 0X15 | 25 0X2C | 56 0X5B | 119 0x2F | 246 0x297 | 501 0X319 | 1012 0xB07 | 2035 0x80F | 2048 0x2055 | 2048 0x43D1 | 2048 0x92ED | 2048 0x755B | ||
| HD=5 | 9 0x39 | 13 0x3AB | 21 0X2B9 | 25 0xBAF | 53 0x1F1 | none | 113 0x4256 | 136 0xD51B | 241 0x5935 | |||||
| HD=6 | 8 0x279 | 12 0X28E | 22 0xA65 | 27 0x683 | 52 0x3213 | 57 0x6E57 | 114 0xAE75 | 135 0X486C | ||||||
| HD=7 | 12 0xAE3 | None | 12 0x254B | 13 0x5153 | 16 0x67AB | 19 0x2D17 | ||||||||
| HD=8 | 11 0xa47 | 11 0x216F | 11 0x46E3 | 12 0xC617 | 15 0x1FB7 | |||||||||
註:上表每一個單元格中有兩個數字,其中上面的數字錶示的是數據幀能達到碼重最大值時地最長的長度,下面的數字就代表在達到這個碼重時採用的具體的生成多項式。
四、方案
從上面的分析我們看到,國際上提供的標準也並不是在任何情況下都能提供很好的差錯檢測性能,因此,針對不同的情況來選擇適當的CRC生成多項式是有必要的,根據以上,我們提供下面的CRC國際標準選擇方案:
1. 當數據幀長度在8bits-128bits範圍內時,推薦CRC-8(CRC-8能夠減少額外比特的開銷,且有更好的性能表現);
2. 當數據幀長度在128bits-2048bits範圍內時,推薦CRC-12,CRC-16,CRC-CCITT(CRC-12額外比特的開銷更小,且用於6bit字元流的傳輸;對於16bits的標準,更推薦美國標準CRC-16,性能略優於CRC-CCITT);
3. 當因數據幀長度更長、通道不穩定等情況而需要更高的性能時,CRC-32、CRC-32C(Castagnoli等人於1993年左右提出的具有更好性能的CRC標準,並被iSCSI、SCTP使用)將是更好的選擇;
4. 選擇其他更多國際標準。
利用多項式,我們定義誤碼多項式E(X)是接收到的消息碼字與正確碼字的異或。即
E(X) = T(X) XOR T(X) …… (14)
則我們容易知道,當且僅當E(X)能夠被CRC多項式P(X)整除的時候CRC演演算法無法檢查到錯誤。當我們選擇一個適當的P(X)時,以下所有差錯E(X)都不能被P(X)整除,因此可以檢測出:
• 單比特差錯,只要P(X)含有一個以上的非零項。
• 雙比特差錯,只要P(X)滿足上述兩種形式((12)(13)式)。
• 任意奇數個比特差錯,只要P(X)含有因式(X - 1)。
• 任意突發差錯,當突發差錯長度小於或等於幀檢驗序列(F(X))的長度(n - k)。
• 長度為(n - k + 1)的突發差錯片段,這個片段等於(1-2)。
• 長度大於(n - k + 1)的突發差錯片段,這個片段等於(1 - 2)
CRC校驗實用程序庫 在數據存儲和數據通訊領域,為了保證數據的正確,就不得不採用檢錯的手段。在諸多檢錯手段中,CRC是最著名的一種。CRC的全稱是循環冗餘校驗,其特點是:檢錯能力強,開銷小,易於用編碼器及檢測電路實現。從其檢錯能力來看,它所不能發現的錯誤的幾率僅為0.0047%以下。從性能上和開銷上考慮,均遠遠優於奇偶校驗及算術和校驗等方式。因而,在數據存儲和數據通訊領域,CRC無處不在:著名的通訊協議X.25的FCS(幀檢錯序列)採用的是CRC-CCITT,WinRAR、NERO、ARJ、LHA等壓縮工具軟體採用的是CRC32,磁碟驅動器的讀寫採用了CRC16,通用的圖像存儲格式GIF、TIFF等也都用CRC作為檢錯手段。下面介紹硬體生成與計算CRC的過程。
下面以最常用的CRC-16為例來說明其生成過程。
CRC-16碼由兩個位元組構成,在開始時CRC寄存器的每一位都預置為1,然後把CRC寄存器與8-bit的數據進行異或,之後對CRC寄存器從高到低進行移位,在最高位(MSB)的位置補零,而最低位(LSB,移位后已經被移出CRC寄存器)如果為1,則把寄存器與預定義的多項式碼進行異或,否則如果LSB為零,則無需進行異或。重複上述的由高至低的移位8次,第一個8-bit數據處理完畢,用此時CRC寄存器的值與下一個8-bit數據異或並進行如前一個數據似的8次移位。所有的字元處理完成後CRC寄存器內的值即為最終的CRC值。
1.設置CRC寄存器,並給其賦值FFFF(hex)。
2.將數據的第一個8-bit字元與16位CRC寄存器的低8位進行異或,並把結果存入CRC寄存器。
3.CRC寄存器向右移一位,MSB補零,移出並檢查LSB。
4.如果LSB為0,重複第三步;若LSB為1,CRC寄存器與多項式碼相異或。
注意:該步檢查LSB應該是右移前的LSB,即第3步前的LSB。
5.重複第3與第4步直到8次移位全部完成。此時一個8-bit數據處理完畢。
6.重複第2至第5步直到所有數據全部處理完成。
7.最終CRC寄存器的內容即為CRC值。
1.《數據與計算機通信》(第十版),William Stallings著,電子工業出版社
2. Wikipedia - 循環冗餘校驗
3.《CRC性能分析及生成多項式選取的研究》,碩士學位論文,鄭州輕工業學院魏艷
