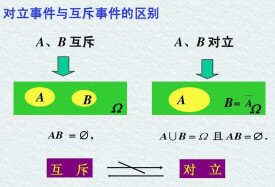
互斥事件
數學中互不相容的事件
事件A和B的交集為空,A與B就是互斥事件。
1、互斥事件定義中事件A與事件B不可能同時發生是指若事件A發生,事件B就不發生或者事件B發生,事件A就不發生。如,粉筆盒里有3支紅粉筆,2支綠粉筆,1支黃粉筆,現從中任取1支,記事件A為取得紅粉筆,記事件B為取得綠粉筆,則A與B不能同時發生,即A與B是互斥事件。
2、對立事件的定義中的事件A與B不能同時發生,且事件A與B中“必有一個發生”是指事件A不發生,事件B就一定發生或者事件A發生,事件B就不發生。如,投擲一枚硬幣,事件A為正面向上,事件B為反面向上,則事件A與事件B必有一個發生且只有一個發生。所以,事件A與B是對立事件,但1中的事件A與B就不是對立事件,因為事件A與B可能都不發生。事件A的對立事件通常記作A。
3、如果事件A與B互斥,那麼事件發生(即A、B中恰有一個發生)的概率,等於事件A、B分別發生的概率的和,即,此公式可以由特殊情形中的既是互斥事件又是等可能性事件推導得到。一般地,如果事件彼此互斥,那麼事件發生(即中有一個發生)的概率,等於這n個事件分別發生的概率的和,即。
4、對立事件是一種特殊的互斥事件。特殊有兩點:其一,事件個數特殊(只能是兩個事件);其二,發生情況特殊(有且只有一個發生)。若A與B是對立事件,則A與B互斥且為必然事件,故發生的概率為1,即。
5、從集合的角度來看,事件A、B互斥,是指事件A所含的結果組成的集合與事件B所含的結果組成的集合的交集為空集,則有;事件A與B對立,是指事件B所含的結果組成的集合,是全集中由事件A所含的結果組成的集合的補集,即,且。
6、公式的常用變形公式為或,在解題中會經常用到。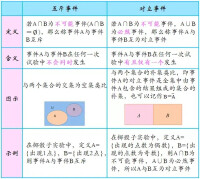

互斥事件
例1.某射手在一次射擊訓練中,射中10環、9環、8環的概率分別為0.24,0.28,0.19,計算這個射手在一次射擊中:
(1)射中10環或9環的概率。(2)不夠8環的概率。
解:(1);(2)
例2.班級聯歡時,主持人擬出了以下一些節目:跳雙人舞、獨唱、朗誦等,指定3個男生和2個女生來參與,把5個人編號為1,2,3,4,5,其中1,2,3表示男生,4,5表示女生。將每個人的號分別寫在5張相同的卡片上,並放入一個箱子中充分混和,每次從中隨機地取出一張卡片,取出誰的編號誰就參與表演節目.
1)為了取出2人來表演雙人舞,連續抽取2張卡片,求取出的2人不全是男生的概率.
2)為了取出2人分別表演獨唱和朗誦,抽取並觀察第一張卡片后,又放回箱子中,充分混合后再從中抽取第二張卡片,求:
i)獨唱和朗誦由同一個人表演的概率;ii)取出的2個不全是男生的概率.
例3.袋中裝有紅、黃、白3種顏色的球各1隻,從中每次任取1隻,有放回地抽取3次,求:
(1)3隻全是紅球的概率,(2)3隻顏色全相同的概率,(3)3隻顏色不全相同的概率。
解:有放回地抽取3次,所有不同的抽取結果總數為33,3隻全是紅球的概率為3隻顏色全相同的概率為
“3隻顏色不全相同”的對立事件為“三隻顏色全相同”.故“3隻顏色不全相同”的概率為
“3隻顏色全不相同”的事件可以分成6個互斥事件,則其概率為6÷33=
若:紅球3個,黃球和白球各兩個,其結果又分別如何?
互斥事件是指事件A和B的交集為空,也叫互不相容事件。也可敘述為:不可能同時發生的事件。如為不可能事件(),那麼稱事件A與事件B互斥,其含義是:事件A與事件B在任何一次試驗中不會同時發生。若A與B互斥,
則互斥事件且;
若a是A的對立事件
則
將較複雜事件表示為若干兩兩互斥事件的和,利用概率加法公式計算互斥事件和的概率,或當一事件的對立事件的概率易求時,將該事件概率的計算轉化為對立事件的概率,簡化計算。解題時應注意互斥事件或對立事件的條件是否滿足。
1.對立事件是互斥事件的特例,所以對立事件一定是互斥事件;
2.互斥事件不一定是對立事件,當且僅當兩個互斥事件必有一個發生時,它們同時又是對立事件;
3.互斥事件和對立事件均不能同時發生。
若為不可能事件,那麼稱事件A與事件B互斥,其含義是:事件A與事件B在任何一次試驗中不會同時發生。
兩者的聯繫在於,對立事件屬於一種特殊的互斥事件。它們的區別可以通過定義看出來。一個事件本身與其對立事件的並集等於總的樣本空間;而若兩個事件互為互斥事件,表明一者發生則另一者必然不發生,但不強調它們的並集是整個樣本空間。即對立必然互斥,互斥不一定會對立。
互斥事件與獨立事件的不同點大致有如下三點:
第一,針對的角度不同.前者是針對能不能同時發生,即兩個互斥事件是指兩者不可能同時發生;後者是針對有沒有影響,即兩個相互獨立事件是指一個事件發生對另一個事件發生的概率沒有影響(注意:不是一個事件發生對另一個事件發生沒有影響)。
第二,試驗的次數不同。前者是一次試驗下出現的不同事件,後者是兩次或多次不同試驗下出現的不同事件。
第三,概率公式不同,若A與B為互斥事件,則有概率加法公式,若A與B不為互斥事件,則有公式;若A與B為相互獨立事件,則有概率乘法公式 。