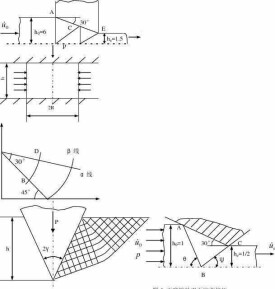
平面應變

學術文獻中的解釋：

1、平面應變是指與分析平面正交的應變等於零的情況。在分析階段的結構分析中沒有計入彈性模量的非線性影響。此外，還可以用等效結構單元PLANE82型來替代上述單元進行結構分析。

2、這類二維變形就稱為平面應變。好些金屬塑性加工過程都可近似地按平面應變分析。

3、考慮一個彈性柱體，取z軸平行於母線，如果應變場滿足條件(1)εx、εy、εxy僅僅是x、y的函數(2)εxz=εyz=εz=0則，這樣的應變狀態稱為平面應變，符合這一條件的力學問題稱為平面應變問題。

金屬材料中平面應變的定義：

在金屬材料斷裂韌度測試的試驗中，對於張開型的裂紋擴展中，在拉伸或彎曲時，其裂紋尖端附近更是處於複雜的應力狀態，最典型的是 平面應變和 平面應力兩種應力狀態。前者出現於厚板中，後者則在薄板中出現。

假設有一無限大板，其中2a長的張開型裂紋，在無限遠處作用有均勻拉應力σ，應用彈性應力學可以分析裂紋尖端附近的應力場、位移場。如用極坐標表示，則各點(r，θ)的應力分量、位移分量可以近似表達如下：

應力分量σz=v(σx+σy)（平面應變）

σz=0(平面應力）

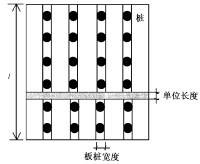
為了能用平面應變有限元來分析砂井地基，首先推導出了砂牆地基(砂井地基在平面應變條件下的表現形式)雙向滲流等應變固結理論解，然後將此解與巴隆軸對稱固結理論解相比較，得到砂井地基平面應變情況和軸對稱情況之間的等效公式。此公式即考慮了地基水平變形，也考慮了砂井的塗抹作用。這種等效方法能方便、準確地用於砂井地基的平面應變有限元分析之中。

砂井(包括砂樁、塑料排水板)排水方法已廣泛地應用於各種軟基處理工程當中。在常規的工程設計中，一般把砂井群地基簡化成單井地基，按軸對稱固結情況來分析其固結過程。若要用有限元來分析，對砂井地基嚴格的講應該採用三維固結有限元來計算。但是三維有限元分析本身的工作量就已相當大，如果再加上密集的砂井而導致劃分的單元大為增加，相比之下，平面問題有限元就要簡便得多，得到廣泛的使用。當然，若直接用平面應變有限元來分析，這顯然是不對的。所以很有必要將砂井地基這種三維繫統(或近似的軸對稱問題)轉換為平面應變問題來處理。其辦法是把原來沿著路基、堤壩等建築物的縱向有一定間隔分佈的砂井想象成沿著縱向連續不間斷分佈的砂牆，即把原來的砂井地基變成打設了一排一排砂牆的地基。而這種砂牆地基就可以當作平面應變問題來分析。再者，在有限元劃分網格時，往往需要在砂井(砂牆)上設置結點，但又不能將一個單元的每個結點均設在砂井上，這就要在砂井中間再劃分一排結點，這將使結點數成倍增加，增加計算工作量。因此還需要放大砂井的間距。但這兩種變換應保證變換前後主要基本量(如固結度)保持不變的前提下進行。有學者推導了等效變換公式，如Shinsya，H.、Hird，C.C.和Indraratna，B.等。對於Shinsya，H.公式應用起來不方便和準確性不好；Hird，C.C.和Indraratna，B.均是從Hansbo理論出發推得的，前者未考慮塗抹作用，後者考慮了塗抹作用，但兩者都沒能考慮地基的側向變形和豎向滲流的影響。我們知道地基的水平向變形在砂井地基的穩定性分析中是一個重要的因素，而且砂井的塗抹作用對固結速率的影響也是不可忽略的。本文將從廣泛使用的巴隆理論出發，既考慮塗抹作用又考慮地基的側向變形和豎向滲流的影響，得到砂井地基平面應變問題和軸對稱問題之間的等效方法。這種等效方法只要調整滲透係數即可，對砂牆的間距可根據網格劃分的需要任意取值。

(1)推導出了考慮塗抹作用砂牆地基雙嚮應變雙向滲流等應變固結解析解，並與巴隆軸對稱解比較，得到砂井地基平面應變問題和軸對稱問題之間的等效方法。這樣只要適當地調整滲透係數，就可以對砂井地基進行平面應變有限元計算。而且砂牆的間距可根據網格劃分的需要任意取值。

(2)對於有豎向排水設置的地基，其固結和滲透方面往往是水平向佔主要方面，因此對水平向滲透係數的調整也是最主要的，而對豎向可以不作調整。這在以上的等效公式中有所反映。

(3)水平向滲透係數的調整係數有可能大於1，也有可能小於1。這是因為在砂牆與砂井分佈的間距相差不大時，砂牆地基的排水能力顯然大於砂井地基的排水能力，固結速率方面砂牆地基要來得快一些，這時在計算中就應該縮小水平向的滲透係數，才能較真實地反映實際地基的固結情況；當計算時所採用的砂牆間距進一步擴大時，砂牆地基的排水能力就有可能小於砂井地基，這時就應該放大滲透係數。有人直接用間距的放大倍數(甚至是倍數的平方)當作滲透係數的調整係數，這樣就會在任何L>1的情況下調整係數總是大於1，這顯然是不對的。

(4)對砂井地基平面應變問題和軸對稱問題之間的等效，無論哪一種方法都不能保證每一點的孔壓對應相等。但能保證兩種情形下固結度和同一深度處平均孔壓在任一時刻相等，這就抓住了地基固結和變形問題的主要方面，完全能滿足實際工程的需要。

描述岩土材料常採用摩爾-庫侖準則和德魯克-普拉格準則，前者的計算結果較為可靠，後者則更便於數值計算。基於非關聯流動法則，推導出平面應變條件下兩種準則相互轉化的關係式，建立了與摩爾-庫侖準則精確匹配的D-P準則。邊坡穩定有限元分析結果表明：與以往各D-P準則及摩爾-庫侖等效面積圓準則相比，建議的匹配D-P準則能更好地反映摩爾-庫侖準則的實際特性，同時，因採用D-P準則的表達形式，也方便了編程計算。

(1)本基於非關聯流動法則建立了與經典的摩爾-庫侖準則相匹配的等效D-P準則，在平面應變的條件下，如果忽略體積變形，可得到D-P參數a，k。邊坡穩定分析的算例表明：與各D-P準則及等效面積圓準則相比，該摩爾匹配D-P準則所得穩定係數更接近常規極限平衡法。

(2)有限元法確定的最危險滑移面與極限平衡法不同，它往往不是一條可以用簡單函數描述的曲線而應是具有一定寬度的滑移帶。

(3)對於有限元法，選用不同的屈服準則並結合強度折減技術得出的塑性區形狀很相似，不同的是塑性應變的大小。無論是採用有限元法還是極限平衡法，對於均質邊坡，兩者得到的最危險滑移面形狀相似。

(4)有限元法的優點不僅僅在於求出折減係數，如果選用的屈服準則合理，對於具有複雜地質地貌的邊坡也可自動求出較為符合實際的臨界滑移面，並能模擬土坡失穩及施工開挖的自然過程，這是傳統極限平衡法無法做到的。當然就有限元法本身來說，其計算精度不僅受邊界條件、網格劃分密度、單元種類的影響，還與具體問題的分析方法及數值收斂性的處理有關，這些問題還有待進一步深入研究。