BP演演算法

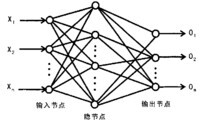
BP（Back Propagation）是一種按誤差逆傳播演演算法訓練的多層前饋網路，是目前應用最廣泛的神經網路模型之一。BP網路能學習和存貯大量的輸入-輸出模式映射關係，而無需事前揭示描述這種映射關係的數學方程。它的學習規則是使用最速下降法，通過反向傳播來不斷調整網路的權值和閾值，使網路的誤差平方和最小。BP神經網路模型拓撲結構包括輸入層（input）、隱層(hide layer)和輸出層(output layer)。

BP神經網路演演算法是在BP神經網路現有演演算法的基礎上提出的，是通過任意選定一組權值，將給定的目標輸出直接作為線性方程的代數和來建立線性方程組的演演算法。

BP演演算法的基本思想是，學習過程由信號的正向傳播與誤差的反向傳播兩個過程組成。正向傳播時，輸入樣本從輸入層傳人，經各隱層逐層處理后，傳向輸出層。若輸出層的實際輸出與期望的輸出(教師信號)不符，則轉入誤差的反向傳播階段。誤差反傳是將輸出誤差以某種形式通過隱層向輸入層逐層反傳，並將誤差分攤給各層的所有單元，從而獲得各層單元的誤差信號，此誤差信號即作為修正各單元權值的依據。這種信號正向傳播與誤差反向傳播的各層權值調整過程，是周而復始地進行的。權值不斷調整的過程，也就是網路的學習訓練過程。此過程一直進行到網路輸出的誤差減少到可接受的程度，或進行到預先設定的學習次數為止。

1986年，Rumelhart和McCelland領導的科學家小組在《Parallel Distributed processing》一書中，對具有非線性連續轉移函數的多層前饋網路的誤差反向傳播（Error Back Proragation，簡稱BP）演演算法進行了詳盡的分析，實現了Minsky關於多層網路的設想。近年來，為了解決BP神經網路收斂速度慢、不能保證收斂到全局最小點，網路的中間層及它的單元數選取無理論指導及網路學習和記憶的不穩定性等缺陷，提出了許多改進演演算法。

1）初始化

2）輸入訓練樣本對，計算各層輸出

3）計算網路輸出誤差

4）計算各層誤差信號

5）調整各層權值

6）檢查網路總誤差是否達到精度要求。滿足，則訓練結束；不滿足，則返回步驟2）

1）非線性映射：足夠多樣本－>學習訓練、能學習和存儲大量輸入-輸出模式映射關係。只要能提供足夠多的樣本模式對供BP網路進行學習訓練，它便能完成由n維輸入空間到m維輸出空間的非線性映射。

2）泛化：輸入新樣本（訓練時未有）->完成正確的輸入、輸出映射

3）容錯：個別樣本誤差不能左右對權矩陣的調整

雖然BP演演算法得到廣泛的應用，但它也存在不足，其主要表現在訓練過程不確定上，具體如下。

(1)訓練時間較長。對於某些特殊的問題，運行時間可能需要幾個小時甚至更長，這主要是因為學習率太小所致，可以採用自適應的學習率加以改進。

(2)完全不能訓練。訓練時由於權值調整過大使激活函數達到飽和，從而使網路權值的調節幾乎停滯。為避免這種情況，一是選取較小的初始權值，二是採用較小的學習率。

(3)易陷入局部極小值。BP演演算法可以使網路權值收斂到一個最終解，但它並不能保證所求為誤差超平面的全局最優解，也可能是一個局部極小值。這主要是因為BP演演算法所採用的是梯度下降法，訓練是從某一起始點開始沿誤差函數的斜面逐漸達到誤差的最小值，故不同的起始點可能導致不同的極小值產生，即得到不同的最優解。如果訓練結果未達到預定精度，常常採用多層網路和較多的神經元，以使訓練結果的精度進一步提高，但與此同時也增加了網路的複雜性與訓練時間。

(4)“喜新厭舊”。訓練過程中，學習新樣本時有遺忘舊樣本的趨勢。

改進的BP演演算法

此前有人提出：任意選定一組自由權，通過對傳遞函數建立線性方程組，解得待求權。本文在此基礎上將給定的目標輸出直接作為線性方程等式代數和來建立線性方程組，不再通過對傳遞函數求逆來計算神經元的凈輸出，簡化了運算步驟。沒有採用誤差反饋原理，因此用此法訓練出來的神經網路結果與傳統演演算法是等效的。其基本思想是：由所給的輸入、輸出模式對通過作用於神經網路來建立線性方程組，運用高斯消元法解線性方程組來求得未知權值，而未採用傳統BP網路的非線性函數誤差反饋尋優的思想。

對給定的樣本模式對，隨機選定一組自由權，作為輸出層和隱含層之間固定權值，通過傳遞函數計算隱層的實際輸出，再將輸出層與隱層間的權值作為待求量，直接將目標輸出作為等式的右邊建立方程組來求解。

現定義如下符號（見圖1）：x（p）輸入層的輸入矢量；y（p）輸入層輸入為x（p）時輸出層的實際輸出矢量；t（p）目標輸出矢量；n，m，r分別為輸入層、隱層和輸出層神經元個數；W為隱層與輸入層間的權矩陣；V為輸出層與隱層間的權矩陣。

具體步驟如下：

（1）隨機給定隱層和輸入層間神經元的初始權值wij。

（2）由給定的樣本輸入xi（p）計算出隱層的實際輸出aj（p）。為方便起見將圖1網路中的閥值寫入連接權中去，令：隱層閥值θj=wnj，x（n）=－1，則：aj（p）=f（■wijxi（p））（j=1，2…m－1）。

（3）計算輸出層與隱層間的權值vjr。以輸出層的第r個神經元為對象，由給定的輸出目標值tr（p）作為等式的多項式值建立方程，

用線性方程組表示為：a0（1）v1r+a1（1）v2r+…+am（1）vmr=tr（1）a0（2）v1r+a1（2）v2r+…+am（2）vmr=tr（2）……a0（p）v1r+a1（p）v2r+…+am（p）vmr=tr（p）簡寫為：Av=T為了使該方程組有唯一解，方程矩陣A為非奇異矩陣，其秩等於其增廣矩陣的秩，即：r（A）=r（A┊B），且方程的個數等於未知數的個數，故取m=p，此時方程組的唯一解為：Vr=[v0r，v2r，…vmr]（r=0，1，2…m－1）

（4）重複第三步就可以求出輸出層m個神經元的權值，以求的輸出層的權矩陣加上隨機固定的隱層與輸入層的權值就等於神經網路最後訓練的權矩陣。

現以神經網路最簡單的XOR問題用VC編程運算進行比較（取神經網路結構為2－4－1型），傳統演演算法和改進BP演演算法的誤差（取動量因子α=0．001 5，步長η=1．653）

BP神經網路演演算法自20世紀80年代提出以來，已經經過了20餘年。除了神經網路理論得到了進一步的發展以外，神經網路的應用成果也日益豐富。神經網路今後發展的一個方向是將其成功地應用於生產、生活的各個方面，發揮其信息處理能力，擴展其應用範圍。

《神經網路設計方法與實例分析》 作者：施彥，韓力群，廉小親 出 版 社：北京郵電大學出版社 ISBN：9787563521029 出版時間：2009-12-01 版次：1

混純系統的模糊神經網路控制理論與方法 作者：譚文 出 版 社：科學出版社 條 形 碼： 9787030212580 ; 978-7-03-021258-0 I S B N ： 9787030212580 出版時間： 2008-5-1

BP演演算法最早由Werbos於1974年提出，1985年Rumelhart等人發展了該理論。BP網路採用有指導的學習方式，其學習包括以下4個過程。

(1)組成輸入模式由輸入層經過隱含層向輸出層的“模式順傳播”過程。

(2)網路的期望輸出與實際輸出之差的誤差信號由輸出層經過隱含層逐層休整連接權的“誤差逆傳播”過程。

(3)由“模式順傳播”與“誤差逆傳播”的反覆進行的網路“記憶訓練”過程。

(4)網路趨向收斂即網路的總體誤差趨向極小值的“學習收斂”過程。

在訓練階段中，訓練實例重複通過網路，同時修正各個權值，改變連接權值的目的是最小化訓練集誤差率。繼續網路訓練直到滿足一個特定條件為止，終止條件可以使網路收斂到最小的誤差總數，可以是一個特定的時間標準，也可以是最大重複次數。

用C語言實現的BP演演算法步驟如下：

1)初始化，用小的隨機數給各權值和閾值賦初值。注意不能使網路中各初始權值和閾值完全相等，否則網路不可能從這樣的結構運行到一種非等權值結構。

2)讀取網路參數和訓練樣本集。

3)歸一化處理。

4)對訓練集中每一樣本進行計算。

①前向計算隱層、輸出層各神經元的輸出。

②計算期望輸出與網路輸出的誤差。

③反向計算修正網路權值和閾值。

5)若滿足精度要求或其他退出條件，則結束訓練，否則轉步驟4)繼續。

6)結果分析與輸出。