懸索
懸掛點之間承受載荷的纜索
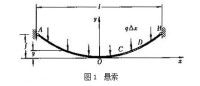
由於懸索的優點是其中各點只承受張力而無彎矩,受力分析比較簡單,因而設計簡便可靠且能充分發揮鋼材性能,以達到節省材料、減輕重量的經濟效果。索系懸掛結構在現代已較廣泛地被採用於某些大跨度的建築結構中。例如懸索橋,其主索AB的兩懸掛點A、B等高,橋面所承受的載荷通過均布的各吊索傳到主索上(圖1)。A、B之間的水平距離l稱為跨度。設每單位水平長度上所受載荷的大小為q,並取坐標系Oxy如圖1所示。略去懸索和吊索的自重,在懸索中任取在x軸上投影長為Δx的一微段CD,該段懸索在張力Ti、Ti+1和鉛垂載荷qΔx作用下平衡(圖2), 因而滿足下述平衡方程:依次類推,可知懸索張力在各點的水平分量都為H,故有:或
。 (3)
由此可得懸索的撓曲形狀為一拋物線,其方程式為:
。
懸索中任意一點的張力。懸索在最低點O處的張力最小,Tx=0=H;在懸掛點處的張力最大
。
懸索最低點與懸掛點之間的鉛垂距離叫垂度,其值
。
載荷沿索長均勻分佈的懸索,如輸電線AB,其單位索長上的載荷為q。在懸索中任取一長為Δs的微段CD,作用在Δs上的鉛垂載荷為qΔs,則平衡方程(1)變為:
。 (4)
水平方向平衡方程與(2)相同。故這種懸索的微分方程為:
(5)
因,故dT=qdy。懸索中任一點的張力為:
T=qy+H,
式中y為該點的縱坐標。可見,兩懸掛點處張力最大。如選取坐標系的原點在懸索的最低點,則(5)之解為:
, (6)
式中是一常數;H是懸索在最低點O處的張力。其撓曲線形狀稱為懸鏈線。將式(6)右邊展開成級數,有:
(7)
如取上式右邊第一項作為近似值,則,為一拋物線。許多國家採用“拋物線”作懸索計算理論。當中央撓度係數n=f0/l0(圖 3)增大到0.08以後,這理論的誤差顯著增大。20世紀60年代,由於大跨距單跨索道、懸掛式屋蓋結構以及大跨度的橋樑等懸索工程設計的需要,中國學者自(7)截取二項作為二次近似理論。懸索曲線為四次代數方程:
。
這樣修改的懸索計算理論同現有的“拋物線”理論比較,能擴大計算範圍兩倍左右。參考書目
懸索圖片

大圖
小圖

小圖