抽樣誤差

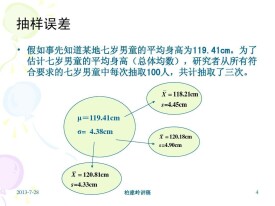
抽樣誤差是指用樣本統計值與被推斷的總體參數出現的偏差。

主要包括：樣本平均數與總體平均數之差，樣本成數與總體成數之差。

統計誤差的來源：一類：登記性誤差；二類：代表性誤差（A、系統性誤差；B、偶然性誤差），抽樣誤差特指偶然性誤差。

抽樣實際誤差是指在一次具體的抽樣調查中，由於隨機因素引起的樣本指標與總體指標之間的離差。如樣本平均數與總體平均數之間的絕對離差，樣本成本與總體成本之間的離差。但是，在抽樣中，由於總體指標數值是未知的，因此，抽樣實際誤差是無法計算的。同時，抽樣實際誤差僅僅是一系列可能出現的誤差數值之一，因此，抽樣實際誤差沒有概括所有可能產生的抽樣誤差。

抽樣平均誤差是指抽樣平均數的標準差或抽樣成數的標準差。從一個總體中我們可能抽取很多個樣本，因此樣本指標如樣本平均數或樣本成本數將隨著不同的樣本而有不同的取值，它們對總體指標如總體平均數或總體成本數的離差有大有小，即抽樣誤差是個隨機變數。而抽樣平均誤差則是反映抽樣誤差的一般水平的一個指標，但由於所有可能樣本平均數的平均數等於總體平均數，樣本成本的平均數等於總體成數，因此，我們不能用簡單算術平均的方法來求抽樣平均誤差，而應採取標準差的方法來計算抽樣平均誤差。

抽樣極限誤差就是指樣本指標與總體指標之間的誤差範圍。

影響抽樣誤差的因素：抽樣單位數的多少，總體中被研究標誌的變動程度的大小。

抽樣誤差是抽樣理論的一個重要概念，在說明抽樣誤差之前我們先介紹統計誤差。統計誤差是指在統計調查中，調查資料與實際情況間的偏差。即抽樣估計值與被估計的未知總體參數之差。例如，樣本平均數與總體平均數之差；樣本成數與總體成數之差等。在統計推斷中，誤差的來源是多方面的，統計誤差按產生的來源分類，有登記誤差和代表性誤差。

登記誤差：

又稱調查誤差或工作誤差，是指在調查過程中，由於各種主觀或客觀的原因而引起的誤差。例如，由於指標含義不清，口徑不同而造成的誤差；由於被調查者提供不實的資料，以及在登記、計算、抄寫上有差錯等而出現的誤差。這種登記誤差不論是在抽樣調查還是在其他形式的調查中都有可能產生。調查的範圍越廣，規模越大，內容越複雜，產生登記誤差的可能性就越大。

代表性誤差：

它是指在抽樣調查中，樣本各單位的結構情況不足以代表總體的狀況，而用部分去推斷總體所產生的誤差。代表性誤差的發生有以下兩種情況：一種是由於違反了抽樣調查的隨機原則。例如，有意識多選好的單位或較差的單位進行調查而造成的系統性誤差。可見，只要遵循了隨機原則就可以避免產生系統性誤差，系統性誤差和登記性誤差一樣，都是抽樣組織工作造成的，應該採取措施預防誤差發生或將其減小到最低程度；另一種情況是指遵循了隨機原則，可能抽到各種不同的樣本而產生的隨機性誤差。隨機性誤差在抽樣推斷中是不避免的，是偶然的代表性誤差。

抽樣誤差：

是指在遵循了隨機原則的條件下，不包括登記誤差和系統性誤差在內的，用樣本指標代表總體指標而產生的不可避免的誤差。由於總體平均數、總體成數是確定的，而樣本平均數、樣本成數是隨機變數，因而抽樣誤差也是一個隨機變數。抽樣誤差越小，說明樣本的代表性越高；反之，樣本的代表性越低。同時抽樣誤差還說明樣本指標與總體指標的相差範圍，因此，它是推斷總體指標的依據。

抽樣誤差是統計推斷所固有的，雖然無法避免，但可以運用數學公式計算。確定其具體的數量界限，並通過抽樣設計程序加以控制，因此抽樣誤差也可以稱為可控制的誤差。

①抽樣單位的數目。在其他條件不變的情況下，抽樣單位的數目越多，抽樣誤差越小；抽樣單位數目越少，抽樣誤差越大。這是因為隨著樣本數目的增多，樣本結構越接近總體。抽樣調查也就越接近全面調查。當樣本擴大到總體時，則為全面調查，也就不存在抽樣誤差了。

②總體被研究標誌的變異程度。在其他條件不變的情況下，總體標誌的變異程度越小，抽樣誤差越小。總體標誌的變異程度越大，抽樣誤差越大。抽樣誤差和總體標誌的變異程度成正比變化。這是因為總體的變異程度小，表示總體各單位標誌值之間的差異小。則樣本指標與總體指標之間的差異也可能小；如果總體各單位標誌值相等，則標誌變動度為零，樣本指標等於總體指標，此時不存在抽樣誤差。

③抽樣方法的選擇。重複抽樣和不重複抽樣的抽樣誤差的大小不同。採用不重複抽樣比採用重複抽樣的抽樣誤差小。

④抽樣組織方式不同。採用不同的組織方式，會有不同的抽樣誤差，這是因為不同的抽樣組織所抽中的樣本，對於總體的代表性也不同。通常，我們不常利用不同的抽樣誤差，做出判斷各種抽樣組織方式的比較標準。