主成分分析

1846年，Bracais提出的旋轉多元正態橢球到“主坐標”上，使得新變數之間相互獨立。皮爾遜（Pearson）（1901）、霍特林（Hotelling）（1933）都對主成分的發展做出了貢獻，霍特林的推導模式被視為主成分模型的成熟標誌。主成分分析被廣泛應用於區域經濟發展評價，服裝標準制定，滿意度測評，模式識別，圖像壓縮等許多領域。

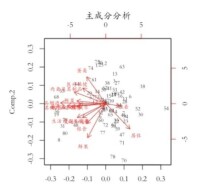
在用統計分析方法研究多變數的課題時，變數個數太多就會增加課題的複雜性。人們自然希望變數個數較少而得到的信息較多。在很多情形，變數之間是有一定的相關關係的，當兩個變數之間有一定相關關係時，可以解釋為這兩個變數反映此課題的信息有一定的重疊。主成分分析是對於原先提出的所有變數，將重複的變數（關係緊密的變數）刪去多餘，建立儘可能少的新變數，使得這些新變數是兩兩不相關的，而且這些新變數在反映課題的信息方面儘可能保持原有的信息。

設法將原來變數重新組合成一組新的互相無關的幾個綜合變數，同時根據實際需要從中可以取出幾個較少的綜合變數儘可能多地反映原來變數的信息的統計方法叫做主成分分析或稱主分量分析，也是數學上用來降維的一種方法。

主成分分析作為基礎的數學分析方法，其實際應用十分廣泛，比如人口統計學、數量地理學、分子動力學模擬、數學建模、數理分析等學科中均有應用，是一種常用的多變數分析方法。

成分分析（包含成分檢測、成分測試項目）是通過微觀譜圖對未知成分進行分析的技術方法，因該技術普遍採用光譜，色譜，能譜，熱譜，質譜等微觀譜圖。

主成分分析是設法將原來眾多具有一定相關性（比如P個指標），重新組合成一組新的互相無關的綜合指標來代替原來的指標。

主成分分析，是考察多個變數間相關性一種多元統計方法，研究如何通過少數幾個主成分來揭示多個變數間的內部結構，即從原始變數中導出少數幾個主成分，使它們儘可能多地保留原始變數的信息，且彼此間互不相關.通常數學上的處理就是將原來P個指標作線性組合，作為新的綜合指標。

最經典的做法就是用F1（選取的第一個線性組合，即第一個綜合指標）的方差來表達，即Var(F1)越大，表示F1包含的信息越多。因此在所有的線性組合中選取的F1應該是方差最大的，故稱F1為第一主成分。如果第一主成分不足以代表原來P個指標的信息，再考慮選取F2即選第二個線性組合，為了有效地反映原來信息，F1已有的信息就不需要再出現在F2中，用數學語言表達就是要求Cov(F1, F2)=0，則稱F2為第二主成分，依此類推可以構造出第三、第四，……，第P個主成分。 

步驟

Fp = a1i*ZX1 + a2i*ZX2 + …… + api*ZXp

其中a1i, a2i, ……,api(i=1,……,m)為X的協方差陣Σ的特徵值所對應的特徵向量，ZX1, ZX2, ……, ZXp是原始變數經過標準化處理的值，因為在實際應用中，往往存在指標的量綱不同，所以在計算之前須先消除量綱的影響，而將原始數據標準化，本文所採用的數據就存在量綱影響[註：本文指的數據標準化是指Z標準化]。

A = (aij)p×m = (a1,a2,…am)，Rai = λiai，R為相關係數矩陣，λi、ai是相應的特徵值和單位特徵向量，λ1 ≥ λ2 ≥ …≥ λp ≥ 0 。

進行主成分分析主要步驟如下：

1. 指標數據標準化（SPSS軟體自動執行）；

2. 指標之間的相關性判定；

3. 確定主成分個數m；

4. 主成分Fi表達式；

5. 主成分Fi命名。 

主成分分析法的基本原理

主成分分析法是一種降維的統計方法，它藉助於一個正交變換，將其分量相關的原隨機向量轉化成其分量不相關的新隨機向量，這在代數上表現為將原隨機向量的協方差陣變換成對角形陣，在幾何上表現為將原坐標系變換成新的正交坐標系，使之指向樣本點散布最開的p 個正交方向，然後對多維變數系統進行降維處理，使之能以一個較高的精度轉換成低維變數系統，再通過構造適當的價值函數，進一步把低維繫統轉化成一維繫統。

主成分分析的原理是設法將原來變數重新組合成一組新的相互無關的幾個綜合變數，同時根據實際需要從中可以取出幾個較少的總和變數儘可能多地反映原來變數的信息的統計方法叫做主成分分析或稱主分量分析，也是數學上處理降維的一種方法。主成分分析是設法將原來眾多具有一定相關性（比如P個指標），重新組合成一組新的互相無關的綜合指標來代替原來的指標。通常數學上的處理就是將原來P個指標作線性組合，作為新的綜合指標。最經典的做法就是用F1（選取的第一個線性組合，即第一個綜合指標）的方差來表達，即Va（rF1）越大，表示F1包含的信息越多。因此在所有的線性組合中選取的F1應該是方差最大的，故稱F1為第一主成分。如果第一主成分不足以代表原來P個指標的信息，再考慮選取F2即選第二個線性組合，為了有效地反映原來信息，F1已有的信息就不需要再出現再F2中，用數學語言表達就是要求Cov（F1,F2）=0，則稱F2為第二主成分，依此類推可以構造出第三、第四，……，第P個主成分。 

主成分分析的主要作用

概括起來說，主成分分析主要有以下幾個方面的作用。

1．主成分分析能降低所研究的數據空間的維數。即用研究m維的Y空間代替p維的X空間(m

2．有時可通過因子負荷aij的結論，弄清X變數間的某些關係。

3．多維數據的一種圖形表示方法。我們知道當維數大於3時便不能畫出幾何圖形，多元統計研究的問題大都多於3個變數。要把研究的問題用圖形表示出來是不可能的。然而，經過主成分分析后，我們可以選取前兩個主成分或其中某兩個主成分，根據主成分的得分，畫出n個樣品在二維平面上的分佈況，由圖形可直觀地看出各樣品在主分量中的地位，進而還可以對樣本進行分類處理，可以由圖形發現遠離大多數樣本點的離群點。

4．由主成分分析法構造回歸模型。即把各主成分作為新自變數代替原來自變數x做回歸分析。

5．用主成分分析篩選回歸變數。回歸變數的選擇有著重的實際意義，為了使模型本身易於做結構分析、控制和預報，好從原始變數所構成的子集合中選擇最佳變數，構成最佳變數集合。用主成分分析篩選變數，可以用較少的計算量來選擇量，獲得選擇最佳變數子集合的效果。