隨機模型
隨機模型
隨機模型亦稱“非確定的、概率的模型”,是按隨機變數建立的模型。其特點是; 模型參數、模擬對象發揮功能的條件和狀態特徵是隨機變數,它們的聯繫方式也是隨機的,或者原始信息以隨機變數來表示。所謂隨機變數就是具有隨機性質的變數。如果希望如實反映系統中隨機變數的因果關係時,就要用隨機模型。例如,保險公司利用年齡作為變數來表示死亡概率的保險統計表就是一種隨機模型。構造隨機模型,需要應用相關分析法、回歸分析法及其他統計方法。在經濟系統中常見的隨機模型有隨機性存貯模型、排隊模型、對策決策模型、馬爾柯夫決策模型等。
英文名:stochastic model
定義:一種非確定性模型,變數之間的關係是以統計值的形式給出的,這類模型稱之為隨機模型。
如果模型中的任一外生變數不確定,並且隨著具體條件的改變而改變,這個模型就被稱為隨機模型。
在現實世界中,不確定現象是普遍存在的。例如,漂浮在液面上的微小粒子不斷地進行著雜亂無章運動,粒子在任一時刻的位置是不確定的;又如公共汽車站等車的人數在任一時刻也是不確定的,因為隨時都可能有乘客的到來和離去。這類不確定現象,表面看來無法把握,其實,在其不確定的背後,往往隱藏著某種確定的概率規律,因此,以概率和數理統計為基礎的隨機模型就成為解決此類問題最有效的工具之一。
靜態隨機模型常見應用有:釣魚問題、報童的策略、電梯問題、經濟軋鋼問題等。
隨機模型是試驗的各處理皆是隨機抽自(圖一)的一組隨機樣本,因而處理效應 τ是隨機的,隨試驗的不同而不同。若重複做試驗,必然是從總體(圖一)中隨機抽取一組新的樣本。其分析的目的不在於研究處理效應,而是在於研究 τ的變異度,故推斷也不是關於某些供試處理,而是關於抽出這些處理的整個總體。所以方差分析要測驗的假設是(圖二)對(圖三)。
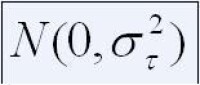
隨機模型
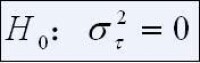
隨機模型
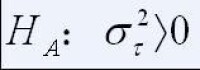
隨機模型
