薄壁結構

薄壁結構是由薄板、薄殼和細長桿件組成的結構，能以較小的重量和較少的材料承受較大的載荷。

木板房屋就是人類早期採用薄壁結構的產物。從18世紀中葉開始，全金屬箱形結構橋樑大量出現。在設計這類橋樑的過程中，S．W．費爾貝恩、E．霍奇金森和Д．И．茹拉夫斯基等人所作的實驗和分析，推動了薄壁結構的力學研究。薄壁結構還應用於船舶和車輛的外殼以及大型建築物的屋頂和屋架。20世紀30年代，飛機飛行速度日益提高，要求飛機有光滑的外形，金屬薄壁結構就取代了蒙布桿繫結構而成為飛行器的主要結構形式。從那個時候起，人們對薄壁結構系統的理論分析和實驗研究．使薄壁結構在工程上得到越來越廣泛的應用。

嚴格地說，薄壁結構的每個桿件都可能受到軸力、剪力和彎矩的作用，每塊板和殼都可能受到彎矩，剪力以及中面內的拉力或壓力的作用。如果全面考慮上述各力的影響，分析和計算就很困難。但多數工程中常用的薄壁結構屬於下面兩類，它們可以簡化為適於數學處理的計算模型。

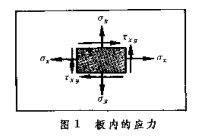
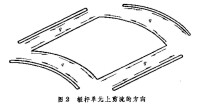
由薄板和細桿組成的薄壁結構，可分解為若干個桿、板單元來研究。其中板只承受板平面內的應力、和 (圖1)，桿只承受軸向力。在很多情況下，桿承受應力的能力遠大於板，進而可以假定板只承受剪應力，而將板所承受的正應力加在桿上(即假想加大桿的截面積)。因板很薄，可認為剪應力置 沿板厚不變，剪應力在整個厚度上的合力用剪流q表示。當板邊為直線時，q的方向與板邊平行；當板邊為曲線時，q的方向與曲線相切。圖2表示出板桿單元上剪流的方向。在板內正應力 = =0的條件下，由平衡條件得出，剪流q在每個邊上為一常值，由整塊板的平衡條件得出，平行四邊形板四個邊上的剪流相等，三角形板三個邊上的剪流均等於零，即不受正應力的三角形板在薄壁結構中不起作用。由於板件邊上的剪流q作用到桿上，桿中的軸力不是常數而按線性規律變化，即桿中相距為l的兩點A、B上的軸力N、N與剪流q的關係為：

N=N+ql 。

因此，通過桿兩端的軸力N、N可求出剪流q。由許多桿和板組成的薄壁結構通常是靜不定結構，一般可用力法通過節點處各桿之間的變形一致條件或桿和板之間的變形一致條件求解。1950年代，J．H．阿吉里斯在這方面做了大量工作，為複雜結構的數值計算開闢了一條新路。目前求解薄壁結構大量採用力法，也越來越多地採用位移法。

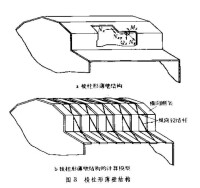
由若干寬度遠小於長度的薄板在長度方向拼接成的稜柱形結構。對這類薄壁結構，蘇聯的B．3．符拉索夫作了下述假設：板主要的內力是中面力N，N、N以及橫向彎矩M和橫向剪力Q(圖3A)；不考慮板的剪應變(見應變)和橫向伸長應變。根據這些假設可以將稜柱形薄壁結構簡化為由許多橫向剛架和縱向鉸結桿件組成的計算模型(圖3B)。在這種計算模型中，彎矩漢沿橫向傳遞。符拉索夫由此得到一些在建築上有廣泛應用的近似解。若稜柱形薄壁結構整個截面的最大尺寸遠小於縱向尺寸，或在橫向有堅硬框架支撐，使結構在受力后不發生顯著的橫向變形，則橫向彎矩M、剪力Q、中面力N和橫向位移均可不考慮，需要研究的只有縱向的中面內力N和剪力N，這兩個內力可通過一個平衡方程相聯繫，因而未知內力只有一個。這種薄壁結構在航空工程和橋樑工程上應用很廣，稱為薄壁梁。

比上述兩種薄壁結構更複雜的結構一般不易簡化。近年來由於大型計算機的普遍使用和計算力學的進展，在分析薄壁結構時可以考慮更多的因素，使越來越多的薄壁結構問題得到解決。