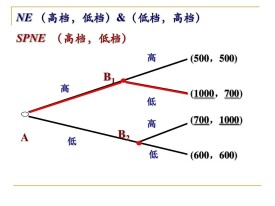
序貫博弈
依序博弈、序貫博弈
序列博弈,也稱為依序博弈、序貫博弈,是指參與者選擇策略有時間先後的博弈形式,每次博弈結構不同而連續多次。因此,某些對局者可能率先採取行動,它是一種較為典型的動態博弈,而重複博弈則可視為一種特殊的動態博弈形式。在序貫博弈中,先行者可能佔據一定的有利地位,我們把它叫做先行者優勢。
序貫博弈是指參與者選擇策略有時間先後的博弈形式。
如果對於每一個參與人i,每一個屬於參與人i的信息集I及其每一個行為策略,存在如下的關係式,那麼對於一個有限擴展式博弈,判斷(p,b)是序貫理性的: 。
如果對於一些信念體系P,判斷(p,b)如上面一樣是序貫理性的,那麼,我們也稱行為策略組合b是序貫理性策略
也就是說,在博弈的任意決策結上(包括未被經過的),沒有參與人有改變其策略的動機,那麼該判斷是序貫理性的。
這樣,序貫理性可以排除圖7.27的(L,m)策略組合。
所以,並非所有的子博弈完美均衡都是序貫理性的,同時也不是所有序管理性行為策略都是子博弈完美均衡。
信念體系p(x)是指在在信息集I(x)上的一個概率分佈,該概率分佈描述了該信息集上的參與人 關於博弈進入該信息集上每一個決策結的的概率(后驗概率)。顯然,這些概率和=1。如上例里p(x)+p(y)=1。
判斷/狀態(p,b)是一對信念體系/行為策略有序組合,給定狀態(p,b),信念p可解釋為給定行為策略b已被採取時,參與人所持有的信念。
在一個合理的狀態中,信念體系p應當是應用貝葉斯法則從既定的行為策略b中推導出來的——當這樣做是可行的,也就是在信息集在均衡路徑上:
如圖7.28 。
貝葉斯法則:信念必定是利用貝葉斯法則由策略中推出的——當這樣做是可行的。
當信息集不在均衡路徑上時,貝葉斯法則不能運用,如圖7.29。這時,可以認為每個決策結上的概率可以取任意值,如圖7.30 。
2、獨立性:信念必定反映出參與人獨立的選擇他們的策略。
3、共同信念:具有相同信息的參與人具有相同的信念。
圖7.30,7.31
滿足1,2,3就是一致的。
定義7.20一致性判斷
對於一個有限的擴展式博弈,如果存在一個完全混合的行為策略的序列bn——他收斂於b,使得貝葉斯法則歸納的信念體系的相關序列pn收斂於p,那麼,判斷(p,b)是一致的。
一致性判斷要滿足貝葉斯法則,獨立性和共同信念。
1、序貫博弈的一般性特徵
一方在決策時,會考慮到另一方的反應行為,並在這種考慮基礎上進行自己的當前決策。
通過對下圖博弈的分析,可以得知廠商1的最佳策略是選擇生產少糖型可樂,廠商2則生產多糖型可樂。
2、首先行動優勢
1)在序貫博弈中,首先作出策略選擇和採取行動的博弈方可以佔據有利地位,獲得較多利益。
2)首先行動優勢的原因在於它造成了一種既成事實,為使利潤最大化,另一方必須根據首先行動一方的策略來選擇自己的策略,而且該模型表明信息較多的博弈方不一定能獲得較多的得益。