勾三股四弦五
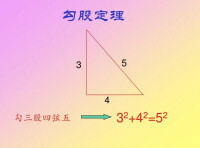
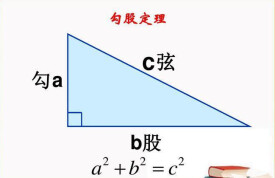
數學中的勾股定理
勾三股四弦五3:4:5
商高,西周初數學家。約與周公旦同時期人。在公元前1000年發現勾股定理的一個特例:勾三,股四,弦五。早於畢達哥拉斯定理五百到六百年。數學成就據《周髀算經》記載,主要有三方面:勾股定理、測量術和分數運算。《周髀算經》中記載了這樣一件事——一次周公問商高:古時作天文測量和訂立曆法,天沒有台階可以攀登上去,地又不能用尺寸去測量,請問數是怎樣得來的?商高回答說:數是根據圓和方的道理得來的,圓從方來,方又從矩來。矩是根據乘、除計算出來的。這裡的“矩”原是指包含直角的作圖工具。這說明了“勾股測量術”,即可用3∶4∶5的辦法來構成直角三角形。《周髀算經》並有“勾股各自乘,並而開方除之”的記載,說明當時已普遍使用了勾股定理。勾股定理是中國數學家的獨立發明,在中國早有記載。《周髀算經》還記載了矩的用途:“周公曰:大哉言數!請問用矩之道。商高曰:平矩以正繩,偃矩以望高,復矩以測深,卧矩以知遠,環矩以為圓,合矩以為方。”據此可知,當時善於用矩的商高已知道用相似關係的測量術。“環矩為圓”,即直徑上的圓周角是直角的幾何定理,這比西方的發現要早好幾百年。