動量矩定理

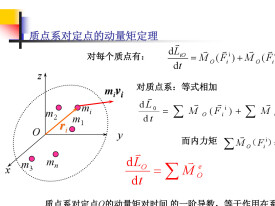
微分形式的動量矩定理定義質點系中第i個質點對某定點O的動量矩為(為第i個質點的矢徑，為第i個質點的動量)，它所受外力對點O的力矩為M，所受內力對點O的力矩為M。將上式的兩側對時間求導數，有。考慮所有質點的合成效果，可得：(1)

式中

為作用於質點系諸外力對點O的力矩的矢量和;

為諸內力對點O的力矩的矢量和。但因內力具有大小相等、方向相反和共線的特點，故

同時，

為質點系對點O的總動量矩，故(1)式可寫作：

(2)

式(2)就是用微分形式表示的動量矩定理，它表明：質點系對某定點O的動量矩對時間的導數等於質點系所受諸外力對該點的力矩的矢量和。若將式(2)兩邊投影到直角坐標軸上，則有：質點系對某定軸的動量矩的時間導數等於質點繫上所受諸外力對相同軸的力矩的代數和。

積分形式的動量矩定理將式（2）改寫成

並進行積分。若LL和L分別表示質點系在時刻和對某點O的動量矩，則

式中為作用於質點i上的外力在時間間隔()內對O點的衝量矩。式(3)就是用積分形式表示的動量矩定理，它表明：在某力學過程的時間間隔內，質點系對某點動量矩的改變，等於在同一時間間隔內作用於質點系所有外力對同一點的衝量矩的矢量和。

對剛體繞定軸z以角速度ω轉動(轉動慣量為Iz)的情況，可將式(3)投影到z軸上，得：，

即在某一時間間隔內，剛體對z軸動量矩()的改變，等於在同一時間間隔內作用於剛體上所有外力對z軸的衝量矩的代數和。

質點是質點系的一個特殊情況，故動量矩定理也適用於質點。

在某力學過程的時間間隔內，質點系對某點動量矩的改變，等於在同一時間間隔內作用於質點系所有外力對同一點的衝量矩的矢量和。

對剛體繞定軸z以角速度ω轉動(轉動慣量為Iz)的情況，可投影到z軸上。

即在某一時間間隔內,剛體對z軸動量矩(Izω)的改變,等於在同一時間間隔內作用於剛體上所有外力對z軸的衝量矩的代數和。

質點是質點系的一個特殊情況，故動量矩定理也適用於質點。

對質心和加速度瞬心使用動量定理時，與對固定點的動量定理具有相同的形式；對質心使用動量矩定理時，無論相對動量的動量矩定理還是絕對動量的動量矩定理，都同對固定點的動量矩定理具有相同的形式；對速度瞬心和速度方向與質心的相對速度相平行的動點，使用絕對動量的動量矩定理以及對加速度瞬心和加速度方向與質心的相對位矢相平行的動點使用相對動量的動量矩定理時，也可得到同對固定點的動量矩定理具有相同的形式；對質心和速度瞬心以及速度方向與質心的相對速度相垂直的動點的動能，都與對固定點的動能形式相同；對質心和加速度瞬心的動能定理與對固定點的動能定理也具有相同的表達形式。