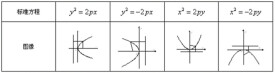
拋物線方程

一種用方程來表示拋物線的方法

拋物線方程就是指拋物線的軌跡方程，是一種用方程來表示拋物線的方法。在幾何平面上可以根據拋物線的方程畫出拋物線。拋物線在合適的坐標變換下，也可看成二次函數圖像。

目錄

1定義 2方程 3解題思路

定義

拋物線定義：平面內與一個定點F 和一條直線l 的距離相等的點的軌跡叫做拋物線，點F叫做拋物線的焦點，直線l叫做拋物線的準線，定點F不在定直線上。它與橢圓、雙曲線的第二定義相仿，僅比值（離心率e）不同，當e=1時為拋物線，當01時為雙曲線。

方程

參數p的幾何意義，是焦點到準線的距離，掌握不同形式方程的幾何性質（如下表）：其中P(x0,y0)為拋物線上任一點。

標準方程	y 2 =2px（p>0）	y 2 =-2px（p>0）	x 2 =2p y（p>0）	x 2 =-2p y（p>0）
圖形	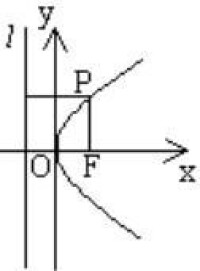拋物線方程	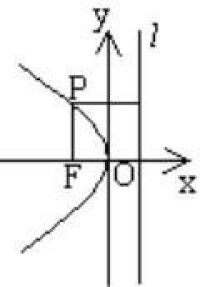拋物線方程	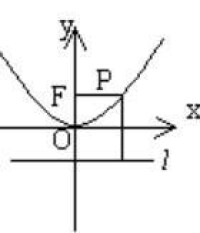拋物線方程	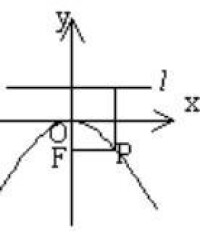拋物線方程
範圍	x ≥ 0， y R	x≤ 0， y R	y ≥ 0， x R	y ≤ 0， x R
對稱軸	X軸		y軸
頂點坐標	原點O(0,0)
焦點坐標	（p/2 ， 0）	（ -p/2， 0）	（ 0，p/2 ）	（ 0，-p/2 ）
準線方程	x=-p/2	x=p/2	y=-p/2	y=p/2
離心率	e = 1
焦半徑	\|PF\|=x0+p/2	\|PF\|=-x0+p/2	\|PF\|=y0+p/2	\|PF\|=-y0+p/2

對於拋物線y^2=2px(p≠0)上的點的坐標可設為(y0^2/2p,y0)，以簡化運算。

拋物線的焦點弦：設過拋物線y2=2px(p>0)的焦點F的直線與拋物線交於A（x1，y1）、B（x2，y2），直線OA與OB的斜率分別為k1,k2，直線l的傾斜角為α。

解題思路

1. 求拋物線方程時，若由已知條件可知曲線是拋物線一般用待定係數法；若由已知條件可知曲線的動點的規律一般用軌跡法。

2. 凡涉及拋物線的弦長、弦的中點、弦的斜率問題時要注意利用韋達定理，能避免求交點坐標的複雜運算。

3. 解決焦點弦問題時，拋物線的定義有廣泛的應用，而且還應注意焦點弦的幾何性質。

考點

拋物線部分是每年高考必考內容，考點中要求掌握拋物線的定義、標準方程以及幾何性質，多出現在選擇題和填空題中，主要考查基礎知識、基礎技能、基本方法，分值大約是5分。

考查通常分為四個層次：

層次一：考查拋物線定義的應用；

層次二：考查拋物線標準方程的求法；

層次三：考查拋物線的幾何性質的應用；

層次四：考查拋物線與平面向量等知識的綜合問題。

解決問題的基本方法和途徑：待定係數法、軌跡方程法、數形結合法、分類討論法、等價轉化法。

目錄