宇稱

假定我們把每一個亞原子粒子都掛上標籤：要麼是A,要麼是B,二者必居其一。再進一步假定，一個A粒子只要分裂成兩個粒子，這兩個粒子要不是統統屬於A類，就必定是統統屬於B類。這時我們可以寫出A=A+A或A=B+B。一個B粒子如果分裂成兩個粒子，這兩個粒子當中總是有一個屬於A類，另一個屬於B類，所以我們可以寫出 B=A十B。你還會發現另一種情形：如果兩個粒子互相碰撞而分裂成三個粒子，這時你就可能發現A+A=A+B+B或A+ B=B+B+B。但是，有些情形卻是觀察不到的。例如，你不會發現A +B=A+A或A+B+A=B+A+B。

為什麼會這樣呢？好吧，讓我們把A看作2,4, 6這類偶數當中的一個，而把B看作3,5,7這類奇數。兩個偶數相加總是等於偶數（6=2+4）,所以A=A+ A。兩個奇數相加也總是等於偶數（8=3+5）,所以A =B+B。但是，一個奇數和一個偶數之和卻總是等於奇數（7=3+4）,所以B=A+B。換句話說，有些亞原子粒子可以稱為“奇粒子”，另一 些亞原子粒子可以稱為“偶粒子”，因為它們所能結合成的粒子或分裂成的粒子正好與奇數和偶數相加時的情況相同。當兩個整數都是偶數或者都是奇數時，數學家就說這兩個整數具有“相同的奇偶性”；如果一個是奇數，一個是偶數，它們就具有“不同的奇偶性（宇稱）”。這樣一來，當有些亞原子粒子的行為象是奇數，有些象是偶數，並且奇數和偶數的相加法則永遠不被破壞時，那就是過去所說的“宇稱守恆”了。 1927年，物理學家魏格納指出，亞原子粒子的宇稱是守恆的，因為這些粒子可以看作是具有“左右對稱性”。真有這種對稱性的東西與它們在鏡子里所成的像（鏡像）完全相同。數字0和8以及字母H和X都具有這樣的對稱性。如果你把8,0,H和X轉一下，讓它們的右邊變成左邊，左邊變成右邊，那麼，你仍舊會得到8,0,H和X。字母 b和p就沒有這種左右對稱性。要是你把它們轉個180°,

b就會變成d，p就變成q——成為完全不同的字母了。 1956年，物理學家李政道和楊振寧指出，在某些類 型的亞原子事件中宇稱應該不守恆，並且實驗很快就證明他 們的說法是對的。這就是說，有些亞原子粒子的行為好像它 們在某些條件下是不對稱似的。由於這個原因，人們研究出了一個更普遍的守恆律。在一個特定粒子不對稱的地方，它的反粒子（即具有相反的電荷或磁場）也是不對稱的，但兩者的模樣相反。因此，如果粒子的形狀象p,它的反粒子的形狀就象q。如果把電荷（C）和宇稱（P）放在一起，就能建立一條簡單的法則，來說明哪些亞原子事件能夠發生，哪些亞原 子事件不能夠發生。這個法則稱為“CP守恆”。後來，人們又明白了，為了使這個法則真正保險，還必須考慮到時間（T）的方向；因為一個亞原子事件看起來既可以是在時間中向前推進，也可以是在時間中向後倒退。添上時間以後的法則稱為“CPT守恆”。

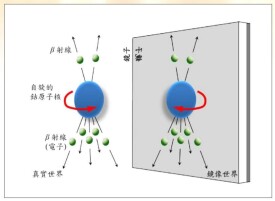
所謂“宇稱”，粗略的說，可理解為“左右對稱”或“左右交換”，按照這個解釋，所謂“宇稱不變性”就是“左右交換不變”。或者“鏡像與原物對稱”。對稱的現象普遍存在於自然界的事物中，事物運動變化的規律左右對稱也是人們的普遍認識。在物理學中，對稱性具有更為深刻的含義，指的是物理規律在某種變換下的不變性。在相當長的一段時間內，物理學家們相信，所有自然規律在這樣的鏡像反演下都保持不變。例如進行牛頓運動定律實驗時，前面放一面鏡子，如果我們看鏡內的物理規律性，則同鏡外完全相同。比如一個小球A向右運動，我們在鏡內看到有一個小球A向左運動，雖然A與A運動方向相反，但它們都遵從的規律，也就是說力學規律對於鏡像反演不變，具有空間反演不變性。同樣對於麥克斯韋方程組和薛定諤方程都具有空間反演不變性。

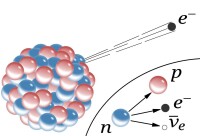
不變性原理通常與守恆定律聯繫在一起，比如動量守恆定律是物理定律在空間平移下的不變性的體現；能量守恆定律與時間平移不變性相聯繫；角動量守恆定律是物理定律空間旋轉對稱性的體現等。在微觀世界中微觀粒子的狀態用波函數ψ描寫即表示波函數的數值隨坐標而變。為了描述這種與空間反演對稱性相聯繫的物理量，引入了“宇稱”的概念。因為連續兩空間反演（鏡像反射）就等於本身，第一次反射，第二次反射。因此宇稱這個量同能量、動量等連續變化的物理量不同，它只能取兩個分立的值（+1）或（-1），也就是說波函數在鏡像對稱時有兩種情形：

第一種情形宇稱為正（+1），第二種情形宇稱為負（-1），對於一個多粒子系統來說，此系統的總宇稱為各該系統粒子的宇稱之乘積。

有了以上概念后，根據左右對稱性就可引伸出“宇稱守恆定律”，表述如下：由許多粒子組成的體系，不論經過相互作用發生什麼變化（包括可能會使粒子數發生變化），它的總宇稱保持不變，則原來為正，相互作用后仍為正；原來為負，相互作用后仍為負。這一定律對於許多情況都是正確的，像強相互作用和電磁相互作用就是如此。因而便認為對於弱相互作用也不言而喻，同樣如此。

弱相互作用下的宇稱守恆的這一看法一直維持了三十年。但在1954~1956年間 人們在粒子物理研究中遇到了一個難題，即所謂的“τ-θ之謎”，就是荷電的κ介子有兩種衰變方式，一種記為τ介子，一種記為θ介子。這兩種粒子的質量、電荷、壽命、自旋等幾乎完全相同，以致於人們不能不懷疑它們是同一粒子。然而另一方面，它們的衰變情形卻不相同，表現為宇稱不相同，當τ粒子衰變時，產生三個π介子，它們的宇稱為負（根椐已確定了的π介子的宇稱為-1和宇稱守恆定律），而θ粒子衰變時產生兩個π介子，它們的宇稱為正，也就是說，τ粒子與θ粒子衰變時具有完全相反的宇稱。

如何解釋這個現象？可供選擇的答案只有兩種：一種承認宇稱守恆定律，則τ粒子與θ粒子是兩種不同的粒子，因為它們的宇稱不同，相互作用過程宇稱應不變，但無法解釋為什麼θ、τ粒子性質如此相同。另一種確認τ和θ是同一種粒，則宇稱守恆定律不成立。

1956年李政道、楊振寧在研究這個問題時，仔細地分析了關於宇稱守恆的各種實驗資料，發現至少在弱相互作用領域，宇稱守恆定律從未得到過實驗的驗證，而只不過是一個理論上的推論而已。因此根據“τ-θ之謎”的啟示，他們提出在弱相互作用過程前後，宇稱可能不守恆，並且還指出可以用β衰變（也是一種弱相互作用）的實驗來證實或否定他們的推測。人們對於弱作用的研究已經有了相當長的歷史，從發現β放射性算起，已經歷了半個多世紀；即使從費米提出β衰變理論算起，也已有二十多個年頭。在這漫長歲月中，人們對於弱作用，尤其對於β衰變，已經作過大量實驗，然而卻沒有一個實驗曾經證明過宇稱是否守恆。這是因為左右對稱性從未有人懷疑過，人們一直相信它，應用它，從未想去檢驗它。當然，要懷疑這樣一條基本定律，必須持非常慎重的嚴肅態度，李政道和楊振寧正是在徹底研究了所有已經作過的弱作用實驗，並發現還沒有一個實驗曾證明過宇稱是否守恆后，才提出弱作用中宇稱可能不守恆的猜測。

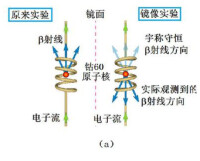
但是，畢竟左右對稱原理太明顯，太自然了，以致人們很難相信宇稱真的會不守恆。著名物理學家泡利就曾俏皮地說過：“我就不相信上帝竟然會是一個左撇子?”究竟宇稱是否守恆，只有讓實驗來作出判斷，為此，李政道和楊振寧設計了一系列可用來檢驗宇稱是否守恆的實驗方案，設計的原則 是要安排兩套實驗裝置，它們嚴格地互為鏡像，然後在這兩套裝置中觀測弱作用過程，看看兩套裝置中出現的是不是互為鏡像的現象。

幾個月之後，以上設想被另一位美籍華裔物理學家吳健雄教授與美國華盛頓國家標準局的幾位物理工作者一起用出色的實驗所證實，這是一個關於極化60Co原子核β蛻變的實驗。在這個實驗中，他們以確鑿無疑的證據表明，在弱相互作用過程中宇稱守恆定律不成立，弱相互作用下宇稱不守恆的發現和實驗驗證，可以說是第二次世界大戰以來最偉大的發現。正是由於這一震驚物理學界的傑出貢獻，李政道和楊振寧共同獲得了1957年諾貝爾物理獎，這時距他們發表宇稱不守恆的研究成果還不到兩年，速度之快在諾貝爾獎金史上是罕見的。