量子數
量子數
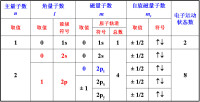
量子數是量子力學中表述原子核外電子運動的一組整數或半整數。因為核外電子運動狀態的變化不是連續的,而是量子化的,所以量子數的取值也不是連續的,而只能取一組整數或半整數。量子數包括主量子數n、角量子數l、磁量子數m和自旋量子數ms四種,前三種是在數學解析薛定諤方程過程中引出的,而最後一種則是為了表述電子的自旋運動提出的。
表徵原子、分子、原子核或亞原子粒子狀態和性質的數。通常取整數或半整數分立值。量
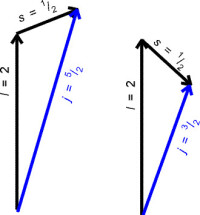
子數是這些粒子系統內部一定相互作用下存在某些守恆量的反映,與這些守恆量相聯繫的量子數又稱為好量子數,它們可表徵粒子系統的狀態和性質。在原子物理學中,對於單電子原子(包括鹼金屬原子)處於一定的狀態,有一定的能量、軌道角動量、自旋角動量和總角動量。表徵其性質的量子數是主量子數n、角量子數l、自旋量子數s=1/2,和總角動量量子數j;在弱磁場中,表徵狀態的量子數要增加總角動量磁量子數mj;在強磁場中,LS耦合解除,表徵其狀態的量子數是主量子數n、角量子數l、其磁量子數ml和自旋磁量子數ms;對於多電子原子(LS情形),單個電子的量子數不是好量子數,表徵原子狀態的量子數是總軌道角動量量子數L、總自旋角動量量子數S以及LS耦合的總角動量子數J。在分子物理學中,分子內部還有振動和轉動,表徵分子狀態除了有電子態的量子數外,還有振動量子數和轉動量子數。在核物理學和粒子物理學中,表徵核和亞原子粒子的狀態和性質有電荷、角動量、宇稱、輕子數、重子數、同位旋及其第三分量、超荷、G宇稱,等等。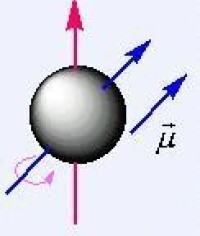

量子數
表徵微觀粒子運動狀態的一些特定數字.量子化的概念最初是由普朗克引入的,即電磁輻射的能量和物體吸收的輻射能量只能是量子化的,是某一最小能量值的整數倍,這個整數n稱為量子數.事實上不僅原子的能量還有它的動量、電子的運行軌道、電子的自旋方向都是量子化的,即是說電子的動量、運動軌道的分佈和自旋方向都是不連續的,此外我們將看到不僅電子還有其它基本粒子的能量、運動軌道分佈、磁矩等都是量子化.
在多電子原子中,軌道角動量量子數也是決定電子能量高低的因素。所以,在多電子原子中,主量子數相同、軌道角動量量子數...上述三個量子數的合理組合決定了一個原子軌道。但要描述電子的運動狀態還需要有第四個量子數—自旋角動量量子數
表示原子內電子運動的能量、角動量、……等的一組整數或半整數。按量子力學原理,原子中核外電子運動、狀態、角動量都不是連續變化的,而是跳躍式變化的,即量子化的。量子數有主量子數、角量子數、磁量子數和自旋量子數。
主量子數
描述電子在原子核外運動狀態的4個量子數之一,習慣用符號n表示。它的取值是正整數,n=1,2,3,……主量
量子數
電子能層為第1(K)、第2(L)、第3(M)、第4(N)、……。氫原子內電子在各能層的能量為:
En=-13.6/n (eV)
n=1,氫原子內電子在第一能層的能量為-13.6電子伏;n=2,氫原子內電子在第二能層的能量為-3.4電子伏;……;n愈大,能量愈高。
角量子數
角量子數決定電子空間運動的角動量,以及原子軌道或電子云的形狀,在多電子原子中與主量子數n共同決定電子
量子數
表示軌道角動量的量子數。角動量用Μl表示:
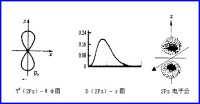
角量子數用l表示,取值為0,1,…,n-1,h為普朗克常數。l值表示原子軌道或電子云的形狀。l=0,原子軌道或電子云是球形對稱的;n=2,l=1,電子云是無把啞鈴形;n=3,l=2,電子云為花瓣形;l=3的電子云形狀更為複雜。光譜學上以 s、p、d、f、…分別表示l=0,1,2,3,…,如n=4,l=0、1、2、3,分別以4s、4p、4d、4f表示。或者說,l表示同一電子能量中的分層。各分層能量高低的關係如下:l值相同而n值不同,則E1S<E2S<E3S;n值相同而l值不同,則E4S<E4P<E4d<E4f。從能量角度看,一個分層代表一個能級。
磁量子數
磁量子數m決定原子軌道(或電子云)在空間的伸展方向。當l給定時,m的取值為從-l到+l之間的一切整數(包括0
量子數
表示軌道角動量方向量子數沿磁場的分量:
Μz=mh/2π
m為磁量子數,取值為0,±1,±2,…,±l,共有2l+1個取值。n=2,l=0,m=0,表明只有一個軌道,即2s;n=2,l=1,m=0,±1,表示有三個空間取向不同的軌道,即2px、2py、2pz。無外加磁場時,三個軌道的能量相同;有外加磁場時,因三個軌道在磁場中的取向不同,表現出較小的能量差別,所以某些線狀光譜分裂成幾條。
自旋量子數
自旋量子數用ms表示。除了量子力學直接給出的描寫原子軌道特徵的三個量子數n、l和m之外,還有一個描述軌道
量子數
通常用向上和向下的箭頭來代表,即↑代表正方向自旋電子,↓代表逆方向自旋電子。
決定電子自旋運動的角動量沿著磁場的分量:
Μs=msh/2π
ms為自旋量子數,取值為±1/2,表明一個軌道上最多只能容納自旋反向的兩個電子。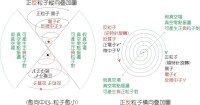

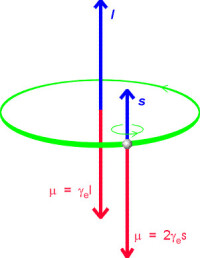
電子的自旋-內部結構模型圖
量子數描述量子系統中動力學上各守恆數的值。它們通常按性質地描述原子中電子的各能量,但也會描述其他物
量子數
最被廣為研究的量子數組是用於一原子的單個電子:不只是因為它在化學中有用(它是周期表、化合價及其他一系列特性的基本概念),還因為它是一個可解的真實問題,故廣為教科書所採用。
在非相對論性量子力學中,這個系統的哈密頓算符由電子的動能及勢能(由電子及原子核間的庫侖力所產生)。動能可被分成,有環繞原子核的電子角動量,J的一份,及餘下的一份。由於勢能是球狀對稱的關係,其完整的哈密頓算符能與J2交換。而J2本身能與角動量的任一分量(按慣例使用Jz)交換。由於這是本題中唯一的一組可交換算符,所以會有三個量子數。
基本粒子包含不少量子數,一般來說它們都是粒子本身的。但需要明白的是,基本粒子是粒子物理學上標準模型

量子數
一般跟時空對稱有關係的量子數有自旋(跟旋轉對稱有關)、宇稱、C-宇稱、T-宇稱(跟時空上的龐加萊對稱有關係)。一般的內對稱有輕子數、重子數及電荷數。條目味有這些量子數的更詳細列表。
值得一提的是較次要但常被混淆的一點。大部分守恆量子數都是可相加的。故此,在一基本粒子反應中,反應前後的量子數總和應相等。然而,某些量子數(一般被稱為宇稱)是可相乘的;即它們的積是守恆的。所以可相乘的量子數都屬於一種對稱(像守恆那樣),而在這種對稱中使用兩次對稱變換式跟沒用過是一樣的。它們都屬於一個叫Z2的抽象群。
