等臂槓桿
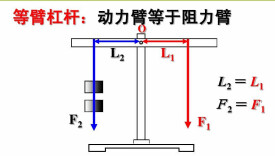
動力臂和阻力臂長度相同的槓桿
槓桿的一種,動力臂和阻力臂長度相同,既不省力也不費力,既不省距離也不費距離。
阿基米德在《論平面圖形的平衡》一書中最早提出了槓桿原理。他首先把槓桿實際應用中的一些經驗知識當作"不證自明的公理",然後從這些公理出發,運用幾何學通過嚴密的邏輯論證,得出了槓桿原理。這些公理是:(1)在無重量的桿的兩端離支點相等的距離處掛上相等的重量,它們將平衡;(2)在無重量的桿的兩端離支點相等的距離處掛上不相等的重量,重的一端將下傾;(3)在無重量的桿的兩端離支點不相等距離處掛上相等重量,距離遠的一端將下傾;(4)一個重物的作用可以用幾個均勻分佈的重物的作用來代替,只要重心的位置保持不變。相反,幾個均勻分佈的重物可以用一個懸掛在它們的重心處的重物來代替;似圖形的重心以相似的方式分佈……正是從這些公理出發,在"重心"理論的基礎上,阿基米德又發現了槓桿原理,即"二重物平衡時,它們離支點的距離與重量成反比。"
阿基米德對槓桿的研究不僅僅停留在理論方面,而且據此原理還進了一系列的發明創造。據說,他曾經藉助槓桿和滑輪組,使停放在沙灘上的桅船順利下水。在保衛敘拉古免受羅馬海軍襲擊的戰鬥中,阿基米德利用槓桿原理製造了遠、近距離的投石器,利用它射出各種飛彈和巨石攻擊敵人,曾把羅馬人阻於敘拉古城外達3年之久。
這裡還要順便提及的是,在我國歷史上也早有關於槓桿的記載。戰國時代的墨家曾經總結過這方面的規律,在《墨經》中就有兩條專門記載槓桿原理的。這兩條對槓桿的平衡說得很全面。裡面有等臂的,有不等臂的;有改變兩端重量使它偏動的,也有改變兩臂長度使它偏動的。這樣的記載,在世界物理學史上也是非常有價值的。
舉例:
天平,定滑輪,蹺蹺板等

等臂槓桿