歐拉法
萊昂哈德·歐拉發明的演演算法
歐拉法(euler method)是以流體質點流經流場中各空間點的運動即以流場作為描述對象研究流動的方法。它不直接追究質點的運動過程,而是以充滿運動液體質點的空間——流場為對象。其中分為前進的EULER法、後退的EULER法、改進的EULER法。
它不直接追究質點的運動過程,而是以充滿運動液體質點的空間——流場為對象。研究各時刻質點在流場中的變化規律。將個別流體質點運動過程置之不理,而固守於流場各空間點。
通過觀察在流動空間中的每一個空間點上運動要素隨時間的變化,把足夠多的空間點綜合起來而得出的整個流體的運動情況。
基本思想是迭代。其中分為前進的EULER法、後退的EULER法、改進的EULER法。所謂迭代,就是逐次替代,最後求出所要求的解,並達到一定的精度。誤差可以很容易的計算出來。
在數學和計算機科學中,歐拉方法(Euler method)命名自它的發明者萊昂哈德·歐拉,是一種一階數值方法,用以對給定初值的常微分方程(即初值問題)求解。它是一種解決常微分方程數值積分的最基本的一類顯型方法(Explicit method)。
微分方程的本質特徵是方程中含有導數項,數值解法的第一步就是設法消除其導數值,這個過程稱為離散化。實現離散化的基本途徑是用向前差商來近似代替導數,這就是歐拉演演算法實現的依據。歐拉(Euler)演演算法是數值求解中最基本、最簡單的方法,但其求解精度較低,一般不在工程中單獨進行運算。所謂數值求解,就是求問題的解y(x)在一系列點上的值y(xi)的近似值yi。對於常微分方程:
\frac{dy}{dx}=f(x,y),x∈[a,b]
y(a) = y0
可以將區間[a,b]分成n段,那麼方程在第xi點有y'(xi) = f(xi,y(xi)),再用向前差商近似代替導數則為:\frac{(y(x_i+1)-y(x_i))}{h}= f(x_i,y(x_i)),在這裡,h是步長,即相鄰兩個結點間的距離。因此可以根據xi點和yi點的數值計算出yi+1來:
y_{i+1}= y_i+ h\times f(x_i ,y_i),i=0,1,2,L
這就是歐拉格式,若初值yi + 1是已知的,則可依據上式逐步算出數值解y1,y2,L。
為簡化分析,人們常在yi為準確即yi = y(xi)的前提下估計誤差 y(xi + 1) − yi + 1,這種誤差稱為局部截斷誤差。
如果一種數值方法的局部截斷誤差為O(hp + 1),則稱它的精度是p階的,或稱之為p階方法。歐拉格式的局部截斷誤差為O(h2),由此可知歐拉格式僅為一階方法。
y(x_i+1)=yi+h \times f(x_i,y_i)
且x_i=x_0+i\times h (i=0,1,2,…,n-1)
局部截斷誤差是O(h2)
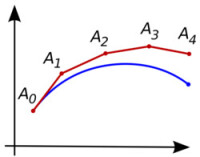
非形式化的幾何詮釋
思路是,一開始只知道曲線的起點,曲線其他部份是未知的,不過通過微分方程,的斜率可以被計算出來,也就得到了切線。
順著切線向前走一小步到點。如果我們假設是曲線上的一點(實際上通常不是),那麼同樣的道理就可以確定下一條切線,依此類推。在經過幾步之後,一條折線就被計算出來了。大部分的情況下,這條折線與原先的未知曲線偏離不遠,並且任意小的誤差都可以通過減少步長來得到(雖然對於剛性方程而言會比較複雜)。
以以下微分方程為例 y'(t) = f(t,y(t)), \qquad \qquad y(t_0)=y_0,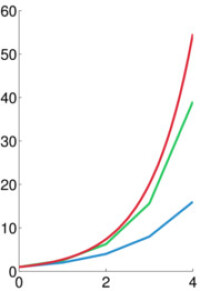

歐拉方法的推導
希望用y 在點(t0,y(t0)) 附近的線性近似來得到其近似解。
利用時間 tn 時的數值,若用單步的歐拉方法,可得到時間tn+1 = ;tn + h 時的近似值如下:
y_{n+1} = y_n + hf(t_n,y_n). \qquad \qquad
歐拉方法是一種顯型方法,也就是說yn + 1 的解是yi, i \leq n 的顯函數。
歐拉方法可以求解一階的微分方程,一個N階的微分方程可以用導入N − 1 個變數來表示y' , y'', ..., y(N) 的方式,分解為N個一階的微分方程。
先用歐拉法求得一個初步的近似值,稱為預報值,然後用它替代梯形法右端的yi+1再直接計算 fi+1,得到校正值yi+1,這樣建立的預報-校正系統稱為改進的歐拉格式:
預報值y~{i+1}=y_i+1 + h \times f(x_i,y_i)
校正值 y_{i+1} =y_i+(\frac{h}{2})\times [f(x_i,y_i)+f(x_i+1,y~i+1)]
它有下列平均化形式:
y_p=y_i+h \times f(x_i,y_i)
且 y_c=y_i+h \times f(x_i+1,y_p)
且 y_{i+1}=\frac{(x_p+y_c)}{2}
它的局部截斷誤差為O(h3),可見,改進歐拉格式較歐拉格式提高了精度,其截斷誤差比歐拉格式提高了一階。
註:歐拉法用差商 \frac{y(x_{i+1})-y(x_i)}{h} 近似代替y(xi)的導數,局部截斷誤差較大;改進歐拉法先用歐拉法求出預報值,再利用梯形公式求出校正值,局部截斷誤差比歐拉法低了一階,較大程度地提高了計算精度。