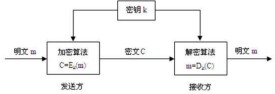
公開密鑰密碼體系

這僅僅是當今密碼學主題的一個方面。對信息發送與接收人的真實身份的驗證、對所發出/接收信息在事後的不可抵賴以及保障數據的完整性是現代密碼學主題的另一方面。

公開密鑰密碼體制對這兩方面的問題都給出了出色的解答，並正在繼續產生許多新的思想和方案。在公鑰體制中，加密密鑰不同於解密密鑰。人們將加密密鑰公之於眾，誰都可以使用；而解密密鑰只有解密人自己知道。迄今為止的所有公鑰密碼體系中，RSA系統是最著名、使用最廣泛的一種。

1976年提出公共密鑰密碼體制，其原理是加密密鑰和解密密鑰分離。這樣，一個具體用戶就可以將自己設計的加密密鑰和演演算法公諸於眾，而只保密解密密鑰。任何人利用這個加密密鑰和演演算法向該用戶發送的加密信息，該用戶均可以將之還原。公共密鑰密碼的優點是不需要經安全渠道傳遞密鑰，大大簡化了密鑰管理。它的演演算法有時也稱為公開密鑰演演算法或簡稱為公鑰演演算法。

1978年提出公共密鑰密碼的具體實施方案，即RSA方案。

1991年提出的DSA演演算法也是一種公共密鑰演演算法，在數字簽名方面有較大的應用優勢。

公鑰體系結構中的一些基本概念與結構組成。

密鑰對在基於公鑰體系的安全系統中，密鑰是成對生成的，每對密鑰由一個公鑰和一個私鑰組成。在實際應用中，私鑰由擁有者自己保存，而公鑰則需要公佈於眾。為了使基於公鑰體系的業務（如電子商務等）能夠廣泛應用，一個基礎性關鍵的問題就是公鑰的分發與管理。

公鑰本身並沒有什麼標記，僅從公鑰本身不能判別公鑰的主人是誰。

在很小的範圍內，比如A和B這樣的兩人小集體，他們之間相互信任，交換公鑰，在網際網路上通訊，沒有什麼問題。這個集體再稍大一點，也許彼此信任也不成問題，但從法律角度講這種信任也是有問題的。如再大一點，信任問題就成了一個大問題。

網際網路路的用戶群決不是幾個人互相信任的小集體，在這個用戶群中，從法律角度講用戶彼此之間都不能輕易信任。所以公鑰加密體系採取了另一個辦法，將公鑰和公鑰的主人名字聯繫在一起，再請一個大家都信得過有信譽的公正、權威機構確認，並加上這個權威機構的簽名。這就形成了證書。

由於證書上有權威機構的簽字，所以大家都認為證書上的內容是可信任的；又由於證書上有主人的名字等身份信息，別人就很容易地知道公鑰的主人是誰。

前面提及的權威機構就是電子簽證機關，即CA。CA（Certificate Authority）也擁有一個證書（內含公鑰），當然，它也有自己的私鑰，所以它有簽字的能力。網上的公眾用戶通過驗證CA（Certificate Authority）的簽字從而信任CA（Certificate Authority），任何人都應該可以得到CA（Certificate Authority）的證書（含公鑰），用以驗證它所簽發的證書。

如果用戶想得到一份屬於自己的證書，他應先向CA（Certificate Authority）提出申請。在CA（Certificate Authority）判明申請者的身份后，便為他分配一個公鑰，並且CA（Certificate Authority）將該公鑰與申請者的身份信息綁在一起，並為之簽字后，便形成證書發給那個用戶（申請者）。

如果一個用戶想鑒別另一個證書的真偽，他就用CA的公鑰對那個證書上的簽字進行驗證（如前所述，CA簽字實際上是經過CA（Certificate Authority）私鑰加密的信息，簽字驗證的過程還伴隨使用CA（Certificate Authority）公鑰解密的過程），一旦驗證通過，該證書就被認為是有效的。

CA（Certificate Authority）除了簽發證書之外，它的另一個重要作用是證書和密鑰的管理。

由此可見，證書就是用戶在網上的電子個人身份證，同日常生活中使用的個人身份證作用一樣。CA（Certificate Authority）相當於網上公安局，專門發放、驗證身份證。

公開密鑰演演算法是在1976年由當時在美國斯坦福大學的迪菲（Diffie）和赫爾曼(Hellman)兩人首先發明的（論文"New Direction in Cryptography"）。但目前最流行的RSA是1977年由MIT教授Ronald L.Rivest,Adi Shamir和Leonard M.Adleman共同開發的，分別取自三名數學家的名字的第一個字母來構成的。

1976年提出的公開密鑰密碼體制思想不同於傳統的對稱密鑰密碼體制，它要求密鑰成對出現，一個為加密密鑰(e)，另一個為解密密鑰(d)，且不可能從其中一個推導出另一個。自1976年以來，已經提出了多種公開密鑰密碼演演算法，其中許多是不安全的，一些認為是安全的演演算法又有許多是不實用的，它們要麼是密鑰太大，要麼密文擴展十分嚴重。多數密碼演演算法的安全基礎是基於一些數學難題，這些難題專家們認為在短期內不可能得到解決。因為一些問題(如因子分解問題)至今已有數千年的歷史了。

公鑰加密演演算法也稱非對稱密鑰演演算法，用兩對密鑰：一個公共密鑰和一個專用密鑰。用戶要保障專用密鑰的安全；公共密鑰則可以發布出去。公共密鑰與專用密鑰是有緊密關係的，用公共密鑰加密的信息只能用專用密鑰解密，反之亦然。由於公鑰演演算法不需要聯機密鑰伺服器，密鑰分配協議簡單，所以極大簡化了密鑰管理。除加密功能外，公鑰系統還可以提供數字簽名。

公鑰加密演演算法中使用最廣的是RSA。RSA使用兩個密鑰，一個公共密鑰，一個專用密鑰。如用其中一個加密，則可用另一個解密，密鑰長度從40到2048bit可變，加密時也把明文分成塊，塊的大小可變，但不能超過密鑰的長度，RSA演演算法把每一塊明文轉化為與密鑰長度相同的密文塊。密鑰越長，加密效果越好，但加密解密的開銷也大，所以要在安全與性能之間折衷考慮，一般64位是較合適的。RSA的一個比較知名的應用是SSL，在美國和加拿大SSL用128位RSA演演算法，由於出口限制，在其它地區（包括中國）通用的則是40位版本。

RSA演演算法研製的最初理念與目標是努力使網際網路安全可靠，旨在解決DES演演算法秘密密鑰的利用公開通道傳輸分發的難題。而實際結果不但很好地解決了這個難題；還可利用RSA來完成對電文的數字簽名以抗對電文的否認與抵賴；同時還可以利用數字簽名較容易地發現攻擊者對電文的非法篡改，以保護數據信息的完整性。

通常信息安全的目標可以概括為解決信息的以下問題：

保密性(Confidentiality)保證信息不泄露給未經授權的任何人。

完整性（Integrity）防止信息被未經授權的人篡改。

可用性（Availability）保證信息和信息系統確實為授權者所用。

可控性（Controllability）對信息和信息系統實施安全監控，防止非法利用信息和信息系統。

密碼是實現一種變換，利用密碼變換保護信息秘密是密碼的最原始的能力，然而，隨著信息和信息技術發展起來的現代密碼學，不僅被用於解決信息的保密性，而且也用於解決信息的完整性、可用性和可控性。可以說，密碼是解決信息安全的最有效手段，密碼技術是解決信息安全的核心技術。

公用密鑰的優點就在於，也許你並不認識某一實體，但只要你的伺服器認為該實體的CA是可靠的，就可以進行安全通信，而這正是Web商務這樣的業務所要求的。例如信用卡購物。服務方對自己的資源可根據客戶CA的發行機構的可靠程度來授權。目前國內外尚沒有可以被廣泛信賴的CA。美國Natescape公司的產品支持公用密鑰，但把Natescape公司作為CA。由外國公司充當CA在中國是一件不可想象的事情。

公共密鑰方案較保密密鑰方案處理速度慢，因此，通常把公共密鑰與專用密鑰技術結合起來實現最佳性能。即用公共密鑰技術在通信雙方之間傳送專用密鑰，而用專用密鑰來對實際傳輸的數據加密解密。另外，公鑰加密也用來對專用密鑰進行加密。

在這些安全實用的演演算法中，有些適用於密鑰分配，有些可作為加密演演算法，還有些僅用於數字簽名。多數演演算法需要大數運算，所以實現速度很慢，不能用於快的數據加密。以下將介紹典型的公開密鑰密碼演演算法-RSA。

RSA演演算法很好的完成對電文的數字簽名以抗對數據的否認與抵賴；利用數字簽名較容易地發現攻擊者對電文的非法篡改，以保護數據信息的完整性。目前為止，很多種加密技術採用了RSA演演算法，比如PGP（PrettyGoodPrivacy）加密系統，它是一個工具軟體，向認證中心註冊后就可以用它對文件進行加解密或數字簽名，PGP所採用的就是RSA演演算法。由此可以看出RSA有很好的應用。

1. 選擇兩個大素數，p 和q ，計算出n=qp，n稱為RSA演演算法的模數。p，q 必須保密，一般要求p，q為安全素數，n的長度大於1024bit ，這主要是因為RSA演演算法的安全性依賴於因子分解大數問題。

2. 計算n的歐拉數

φ(n)=(p-1)(q-1)

φ(n)定義為不超過n並與n互質的數的個數。

3. 然後隨機選擇加密密鑰e，從[0,φ(n)-1]中選擇一個與φ(n)互質的數e作為公開的加密指數。

4. 最後，利用Euclid 演演算法計算解密密鑰d, 滿足de≡1(mod φ(n))。其中n和d也要互質。數e和n是公鑰，d是私鑰。兩個素數p和q不再需要，應該丟棄，不要讓任何人知道。

5.得到所需要公開密鑰和秘密密鑰：

公開密鑰（即加密密鑰） PK=（e，n）

秘密密鑰（即解密密鑰） SK=（d，n）

1. 加密信息 m（二進位表示）時，首先把m分成等長數據塊m1 ,m2,..., mi ，塊長s，其中 2^s <= n, s 儘可能的大。

2. 對應的密文是：ci ≡mi^e ( mod n ) ( a )

3. 解密時作如下計算：mi ≡ci^d ( mod n ) ( b ) RSA 可用於數字簽名，方案是用 ( a ) 式簽名， ( b )式驗證。