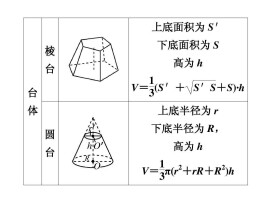
台體體積公式

V台體=1/3h(S上+√(S下·S上)+S下)

當S上=S下時:

V柱=S·h

當S上=0時：柱體積公式推導圖V錐=1/3S·h

都可根據台體體積推得."S上"為台體上體面,"S下"為台體下底面,"h"為高.

本人推導出在非標準狀態下更正確的體積公式

底面a﹒b，頂面c﹒d，高h

體積公式：v=1/2(a﹒b+c﹒d)h－1/6(a-c)(b-d)h

完全適用於錐體、柱體、稜台（不需要是正稜台）

在稜柱狀態下，底面與頂面a=c，b=d，

則體積公式簡化後為v=a﹒b﹒h

在正稜錐狀態下，頂面面積為0，並且是c=0,d=0.

則體積公式簡化為 v=1/2a﹒b﹒h－1/6a﹒b﹒h=1/3a﹒b﹒h

在非標準狀態下稜台體積如頂面為只有長沒有寬狀態下的刃型體積(如橫放

的三稜柱）

頂面c=a，d=0正稜台體積推導v=1/2a﹒b﹒h （用三稜柱立式來算也是該結果）像這種非標準狀態恰恰是現有公式根本無法計算的（只要不立起來算）

當稜台為正稜台時，簡化公式為：相當於底面、頂面均為正方型，即a=b,c=d；

v=1/2(a^2+c^2)h-1/6(a-c)(a-c)h=1/3h(a^2+c^2+2a﹒c)

與標準狀態下的稜台計算公式完全吻合。對於圓台也是一樣，只不過將圓理解成正方形（即πr^2理解成邊長為r√π .）

對於很特殊體積計算一樣有效：

如底面面積為0，頂面面積為0的體積計算高為h(其實是一個非標的四面體）

b=0,c=0

v=1/6adh

這恐怕標準的稜台公式是怎麼也無法計算的，因為底面積為0，頂面積也為0，按照公式推導只能是0，而其實是有這樣的實物的，就是一個四面體