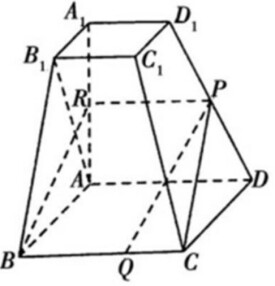
稜台
稜錐的底面和平行於底面的一個截面間的部分
稜錐的底面和平行於底面的一個截面間的部分,叫做稜台。由三稜錐,四稜錐,五稜錐,……等截得的稜台,分別叫做三稜台,四稜台,五稜台,……等。由正稜錐截得的稜台叫做正稜台。正三稜台,正四稜台,正五稜台,……等。
正稜台的性質:
(1)正稜台的側棱相等,側面是全等的等腰梯形。各等腰梯形的高相等,它叫做正稜台的斜高;
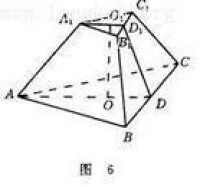
稜台
(3)正稜台的兩底面中心連線、相應的邊心距和斜高組成一個直角梯形;兩底面中心連線、側棱和兩底面相應的半徑也組成一個直角梯形。
(4)稜台各棱的反向延長線交於一點。
兩個平行的面分別叫做上底面和下底面,其餘的面叫做側面,側面相交的線段叫做側棱,3條側棱相交的點叫做頂點。
正稜台各側面的高叫做稜台的斜高。
稜錐的底面和平行於底面的一個截面間的部分,叫做稜台(léng tái)
稜台的體積取決於兩底面之間的距離(稜台的高),以及原來稜錐的體積。設h為稜台的高,和為稜台的上下底面積,V為稜台的體積。由於稜台是由一個平面截去稜錐的一部分(也就是和原來稜錐相似的一個小稜錐)得到,所以計算體積的時候,可以先算出原來稜錐的體積,再減去和它相似的小稜錐的體積。稜錐被平行於底面的平面所截時,截面的面積與底面面積的比,等於小稜錐和原稜錐的高的比的平方。假設原稜錐的高是H,那幺小稜錐的高是H-h。也就是說:
稜台的體積公式:
S:上底面積
:下底面積
h:高
即
稜台的底面和頂面近似時,稜台的上底面面積S加下底面面積除以2的平均面積的一個乘以高h,就是稜台體積: