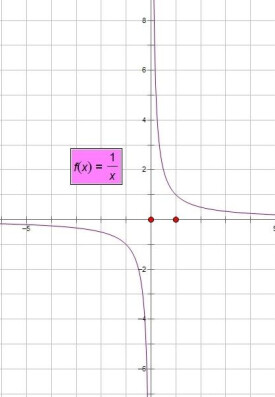
無界函數

無界函數的定義：對任意的且小於正無窮，存在x,使得，則f(x)無界。典型的例如等都是無界函數。

1.無界函數與無窮大量兩個概念之間有嚴格的區別：

無界函數的概念是指某個區間上的。若對於任意的正數，總存在某個點，使得，則稱該函數是區間上的無界函數。

無窮大量是指在自變數的某個趨限過程(例)下因變數的變化趨勢。若對於任意正數，總存在，對一切滿足的，總有，則稱函數是時的無窮大量。

無窮大量必是無界量，無界量未必是無窮大量。

舉例：有函數,則此函數為無界函數，但不為無窮函數。因為當X趨於無窮時，函數值關於X軸上下擺動，總有某點，所以不為無窮。

定義1 設函數的定義域為D，若存在一個常數，使得，都有

則稱為D內有上(下)界的函數，數M(L)稱為在D內的一個上(下)界。

定義2 設函數若存在一個正數，使得，都有

則稱在D內是有界函數；否則，稱為無界函數。

有界函數的等價定義是：若在D內既有上界又有下界，則稱在D內是有界函數。

在D內有界當且僅當數集是有界集，即

其中M，L為常數，分別稱為的一個上界和一個下界。

無界的正面描述是：

是無界函數當且僅當，使得。

有界函數的幾何意義：

若函數為有界函數，則的圖像

完全落在直線之間。

注意：函數的有界性與函數自變數x的取值範圍有關，如：，在R內無界，但在任何有限區間內都有界。

有界函數的圖形必介於兩條平行於x軸的直線之間（當自變數為x時），籠統地說某個函數是有界函數或無界函數是不確切的，必須指明所考慮的區間。

例如，函數在內是有界的，因為對任意，存在，使得恆成立。

函數在開區間上是無界的。

函數在開區間內是無界的，而函數在區間內是有界的。

函數是有界函數，因為在其定義域內恆有