切比雪夫定理
切比雪夫定理
切比雪夫定理,19世紀俄國數學家切比雪夫,研究統計規律中,論證並用標準差表達了一個不等式,這個不等式具有普遍的意義。

切比雪夫
所有數據中,至少有3/4(或75%)的數據位於平均數2個標準差範圍內。
所有數據中,至少有8/9(或88.9%)的數據位於平均數3個標準差範圍內。
所有數據中,至少有24/25(或96%)的數據位於平均數5個標準差範圍內。
意義切比雪夫不等式說明,DX越小,則 P{|X-EX|>=ε} 越小,P{|X-EX|<ε}越大,也就是說,隨機變數X取值基本上集中在EX附近,這進一步說明了方差的意義。
切比雪夫不等式可以使人們在隨機變數X的分佈未知的情況下,對事件 概率作出估計。
定理
設隨機變數X具有數學期望,方差 則對任意正數ε,不等式 或 成立。
注意:應用切比雪夫不等式必須滿足E(X)和D(X)存在且有限這一條件。
若對於任意的ε>O,當n很大時,事件“ ”的概率接近於0,則稱隨機變數序列{Xn}依概率收斂於a 。正因為是概率,所以不排除小概率事件“”發生。所以,依概率收斂是不確定現象中關於收斂的一種說法,記為。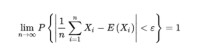
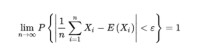
切比雪夫定理
切比雪夫定理
設X1,X2,…,Xn,…是相互獨立的隨機變數序列,數學期望E(Xi)和方差D(Xi)都存在(i=1,2,…),且D(Xi)0,有
特別地:X1,X2,…,Xn,…是相互獨立的隨機變數序列,數學期望E(Xi)=μ和方差D(Xi)=σ(i=1,2,…),則對任意給定的ε>0,有
即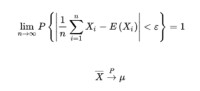 切比雪夫定理的這一推論,使我們關於算術平均值的法則有了理論根據.設測量某一物理量a,在條件不變的情況下重複測量n次,得到的結果X1,X2,…,Xn是不完全相同的,這些測量結果可看作是n個獨立隨機變數X1,X2,…,Xn的試驗數值,並且有同一數學期望a。於是,按大數定理j可知,當n足夠大時,下式成立,即
切比雪夫定理的這一推論,使我們關於算術平均值的法則有了理論根據.設測量某一物理量a,在條件不變的情況下重複測量n次,得到的結果X1,X2,…,Xn是不完全相同的,這些測量結果可看作是n個獨立隨機變數X1,X2,…,Xn的試驗數值,並且有同一數學期望a。於是,按大數定理j可知,當n足夠大時,下式成立,即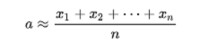
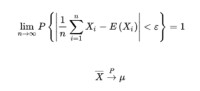
切比雪夫定理
切比雪夫定理
上式表明,n足夠大時,把n次測量結果的算術平均值作為a的近似值,所產生的誤差是很小的。
