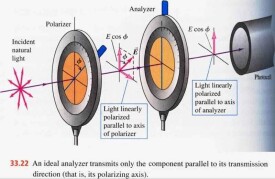
馬呂斯定律
1808年馬呂斯提出的定律
馬呂斯指出:強度為Io的線偏振光,透過檢偏片后,透射光的強度(不考慮吸收)為I=Io(cos)^2。(是入射線偏振光的光振動方向和偏振片偏振化方向之間的夾角。)

馬呂斯
按電磁波理論,光是橫波,它的振動方向和光的傳播方向垂直。在垂直於光波傳播方向的平面內,光矢量可能有不同的振動方向,通常把光矢量保持一定振動方向上的狀態稱為偏振態。
由起偏器產生的偏振光在通過檢偏器之後,如圖,OM表示起偏器的偏振化方向,ON表示檢偏器的偏振化方向,它們的夾角為α。自然光透過起偏器后成為沿OM方向的線偏振光,設其振幅為E0,而檢偏器只允許它沿ON方向的分量通過,所以從檢偏器透出的光的振幅為
E=E0cosα
由此可知,若入射檢偏器的光強為I0,則檢偏器射出的光強與原光強及偏振器角度存在一定關係。
1808年,馬呂斯經實驗指出,強度為Io的線偏振光,透過檢偏片后,透射光的強度(不考慮吸收)為:
I=Io(cosα)^2
其中, α是入射線偏振光的光振動方向和偏振片偏振化方向之間的夾角。
一束光強為Io的線偏振光,透過檢偏器以後,透射光的光強為I=Io(cosα)^ 2 。式中α是線偏振光的光振動方向與檢偏器透振方向間的夾角,該式稱為馬呂斯定律。
在光路中放入偏振片P1 作為起偏器,獲得振動方向與P1透振方向一致的線偏振光,線偏振光的強度為入射自然光強度的一半。
在光路中放入偏振片P2 ,作為檢偏器,其透振方向P2與P1 夾角為,透過P2的光振幅:E=Eo(cosα),光強:I=Io(cosα)^2 , 這就是馬呂斯定律。
當α=0°或180°時,I=Io ,透射光最強。當α=90°或270°時,I=0,透射光強為零。當為其它值時,光強介於 0 和Io之間。
簡單原理:兩偏振片的透振方向之間夾角為α,透過起偏器的偏振光振幅為Ao,則透過檢偏器的振幅為A,則A=Aocosα
因為探測器檢測到的是光強,光強為I=A^2
可得I=(Aocosα)^2=Io(cosα)^2
兩個偏振片緊靠在一起,將它們放在一盞燈的前面以至沒有光通過,如果將其中的一片旋轉180°,在旋轉的過程中,將會產生什麼現象呢?
解答:透過偏振片的光強先增強,然後又減小為零。
再問:平行時最強,90°時無光,那麼30°呢,60°呢,除了平行和垂直情況以外,其他偏角時刻透過的光強情況又如何呢?
根據馬呂斯定理30°的時候:I =四分之三 I0
60°的時候:I = 四分之一 I0
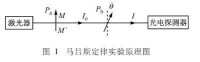
圖 1 馬呂斯定律實驗原理圖
I = I0 cos^2 θ( 1)
起偏器P a 產生一線偏振光, 強度為I0, 其透振方向為MM',通過檢偏器P b 后, 按照馬呂斯定律其透射光強為I = I0 cos^2 θ。為了定量地檢測透射光強的大小, 在P b 後放一光電池, 根據光電池的輸出電流i與透射光強大小I 成正比的關係, 可知光電池輸出電流為
i = kI ( 2)
由( 1)、( 2) 易知
i = i0 cos^2 θ ( 3)
其中i0 = kI0。因此, 光電池的輸出電流i與偏振片的透振方向夾角θ為餘弦平方關係。
WGZ-Ⅱ型光強分佈測試儀配有起偏、檢偏裝置和光電探頭及數字檢流計, 可以在垂直於光傳播方向的
平面內方便地調整檢偏器轉角θ, 實驗光路如圖2所示。
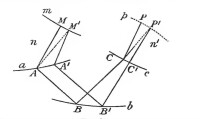
證明馬呂斯定律
設同源光束[MABCP]與[M'A'B'C'P']與曲面m分別在M,M'點正交;這兩道光線在傳播過程中經過多次反射或折射,分別與界面a相交於A,A'點;與界面b相交於B,B'點,與界面c 相交於C,C'點;經過若干反射、折射後分別到達P,P'點;令光線[MABCP]、[M'A'B'C'P'] 的光程相等;則所有等光程的P,P'的集合,形成一個曲面p。可證明光線[MABCP]與曲面p在P點正交,光線[M'A'B'C'P']與曲面p在P'點正交,即集合p是光束的正交一致性曲面。
證:
作兩條附加直線M'A和P'C。令M與M'無限接近,因M'A與曲面m 垂直,光線[M'ABCP']與光線[M'A'B'C'P']之差是MM'線段的高次微小項
即[M'ABCP']~[M'A'B'C'P']。但根據費馬原理的要求,[M'A'B'C'P]=[MABCP],代入前式,可得
[M'ABCP']=[MABCP];
令第一介質和最後介質的折射率分別為n,n',則消除共同線段之後可得:
由此
在M和M'無限接近時M'A=MA,於是 CP'=CP;即CP,CP'是等腰三角形的兩腰,與PP'夾角相等;當其無限接近時CP,CP'合為一體,垂直於曲面p。同理可證C'P'垂直於p。 。
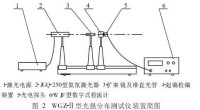
圖 2 WGZ-Ⅱ型光強分佈測試裝置簡圖