共找到2條詞條名為互補色的結果 展開
- 混合后而能產生白光的兩種顏色
- 拮抗理論
互補色
混合后而能產生白光的兩種顏色
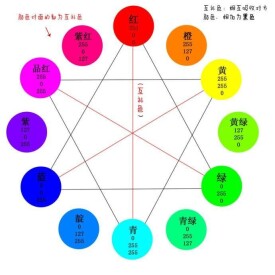
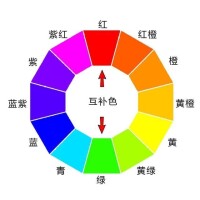
互補色分美術互補色和光學互補色兩種。美術互補色定義,色相環中成180°角的兩種顏色。光學互補色定義,兩種色光以適當比例混合產生白光。
互補術互補義略差異,導致互補系略差異
量紅+綠=黃,互補藍光;
量紅+藍=品紅(稱洋紅,即較淺紫紅),互補綠;
等量的綠光+藍光=青光,互補於紅光。
如果三原色光中某一種色光與某一種三原色光以外的色光等量相加后形成白光,則稱這兩種色光為互補色光。互補色光之間,能夠形成相互阻擋的效果。於是可知以下三對互補色光:黃光與藍光、紅光與青光、綠光與品紅光。
色彩中的互補色相互調和會使色彩純度降低,變成灰色。一般作畫的時候不用補色調和。
不過在兩種顏色互為補色的時候,一種顏色占的面積遠大於另一種顏色的面積的時候,就可以增強畫面的對比,使畫面能夠很顯眼。一般情況下,補色運用有得有失。
互補色
德國生理學家黑林(EwaldHerring)於19世紀50年代提出顏色的互補處理(opponentprocess)理論。他不同意流行的楊-赫爾姆霍茲的三色素理論,認為人眼中有三對互補色處理機制,三對互補色是:藍黃,紅綠,黑白。每一對中兩種不能同時出現,兩種互補,只能有一種佔上風。三對互補機制輸出的信號大小比例不同,人眼色覺就不同。黑林提出這種理論是因為受到顏色負后象現象的支持。顏色負后象現象比如,長久注視紅花之後,再觀看白色背景,你會看到青色的花。先注視紅花上的“十”字半分鐘,在看白紙,白紙上就會隱約顯示出青色的花來。如果花是黃的,白紙上就會顯示出藍色花,如果花是絳色,白紙上會顯示出綠色花。
按照黑林的意思,紅綠是一對互補色,兩種色光相加等於白色。而按照我們日常對“紅”、“綠”的用法,紅綠兩種色光相加等於黃色光,而不是白色光,所以,或一對介於兩者之間的互補色。澄清這一點非常重要(後面我們談到流行的階段模型時還要談到)。
用黑林的理論可以這樣解釋負后象現象:當人眼長久注視紅色時,“紅綠”(紅青)機制中性點向綠色方向偏移,以至白色變成“綠色”(青色)。其實三色素理論解釋負后象現象更加直觀:當人眼長久注視紅色時,紅色敏感細胞敏感性降低,以至白色顯現出青色,即(B,G,R)由(1,1,1)變成(1,1,1-Δ);而(1,1,1-Δ)可以分解成白色(1-Δ,1-Δ,1-Δ)和青色(Δ,Δ,0)。
非發光物體的顏色(如顏料),主要取決於它對外來光線的吸收和反射,所以該物的顏色與照射光有關。一般把物體在白晝光照射下所呈現的顏色稱為該物體的顏色。如果將白晝光照射在黃藍兩種顏色混合后的表面時.因黃顏料能反射白光中的紅、橙、黃和綠四種色光,而藍色光能吸收其中的紅、橙和黃三種色光,結果使混合顏料顯示綠色。這種顏色的混合與色光的加色混合不同。
互補色
色盲分為全色盲和部分色盲(紅色盲、綠色盲、藍黃色盲等)。色弱包括全色弱和部分色弱(紅色弱、綠色弱、藍黃色弱等)。
1.全色盲
屬於完全性視錐細胞功能障礙,與夜盲(視桿細胞功能障礙)恰好相反,患者尤喜暗、畏光,表現為晝盲。僅有明暗之分,而無顏色差別,而且所見紅色發暗、藍色光亮。此外,還有視力差、弱視、中心性暗點、擺動性眼球震顫等癥狀。它是色覺障礙中最嚴重的一種,較少見。
2.紅色盲
又稱第一色盲。患者主要是不能分辨紅色,對紅色與深綠色、藍色與紫紅色以及紫色不能分辨。常把綠色視為黃色,紫色看成藍色,將綠色和藍色相混為白色。
3.綠色盲
又稱第二色盲,患者不能分辨淡綠色與深紅色、紫色與青藍色、紫紅色與灰色,把綠色視為灰色或暗黑色。臨床上把紅色盲與綠色盲統稱為紅綠色盲,較常見。平常說的色盲一般就是指紅綠色盲。
4.藍黃色盲
又稱第三色盲。患者藍黃色混淆不清,對紅、綠色可辨,較少見。
5.全色弱
又稱紅綠藍黃色弱。其色覺障礙比全色盲程度要低,視力無任何異常,也無全色盲的其他併發症。在物體顏色深且鮮明時則能夠分辨;若顏色淺而不飽和時則分辨困難,少見。
6.部分色弱
有紅色弱(第一色弱)、綠色弱(第二色弱)和藍黃色弱(第三色弱)等,其中紅綠色弱較多見,患者對紅、綠色感受力差,照明不良時,其辨色能力近於紅綠色盲;但物質色深、鮮明且照明度佳時,其辨色能力接近正常。
互補色
由於黑林理論有某種長處,20世紀50年代,在美國心理學家Hurvich和Jameson的推崇之下,黑林理論重新得到重視。一種結合兩種理論的階段模型因此產生。按照這種理論,顏色信號在視細胞階段以三色素形式(即B,G,R形式)存在,而在神經節細胞――視網膜輸出信號的細胞――以互補色形式存在。視覺機制首先由B,G,R三色信號得到黃色和白色信號Y和W,B-Y得到藍黃互補色信號,R-G得到紅綠互補色信號,W和適應色或背景色信號相減,得到黑白互補信號。
流行的階段模型--Walraven模型
這個模型有這樣幾個問題:
(1)“紅”、“綠”的使用,前後不一致,如果紅加綠等於黃,那麼兩者就不是黑林理論中的互補色,兩者相減是無意義的。
(2)顏色相加是矢量相加,而不是分量相加,R+G和B+G+R不具有任何意義。由這樣的加法也得不出黃色信號或白色信號。
由於上述原因,網上有些階段模型假設B,G,R三者的線性組合(三者乘上不同的係數后相加減)產生紅綠互補信號。有些模型也不再強調中間的黃色信號產生。但是這樣一來,階段模型的互補處理就變成線性組合處理了。