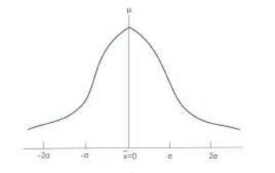
高斯曲線

卡爾·弗里德里奇·高斯（Carl Friedrich Gauss）在格丁根（Gottingen）的那座天文台是大約於1807年建成的。在他的整個一生中，從那時起：近200年的大部分時間裡，天文儀器不斷得到改進。我們今天所看到的一顆星辰的位置，在當時已被人們多次確定，因此，在我們看來，我們的觀察似乎越來越趨於精確。但是，當我們將各次觀察結果加以比較時，我們就會驚奇而懊喪地發現，它們仍然散亂無序。人們曾經希望觀察的偏差終會消失，人們也會像上帝那樣洞燭幽微的。但是，事實上，錯誤仍無法從觀察中根除。無論是觀察群星、原子、人的照片，還是聽某人的講演，都是這樣。

GraphView中的高斯函數方程：y=1/(0.4sqrt(2pi))e^(-0.5((x-1)/0.4)^2)

高斯以他那令人驚嘆的、孩子氣的天才意識到了這一點。直到他80歲高齡與世長辭時，仍然保持了這種天才。1795年，18歲的高斯進入格丁根大學讀書，其時他已經解決了有關一系列觀察中固有的誤差的最佳估算問題。

當一位觀察者在觀察一顆星時，他知道有大量的致誤因素。於是，他閱讀若干觀察記錄，自然希望這顆星的位置的最佳估計是一個平均數——即散布的中心。迄今為止，這一點不言自明。然而，高斯卻要進一步研究這種誤差的分佈告訴了人們什麼。他提出了高斯曲線（the Gaussian curve），使這種離散性可以由這種曲線的偏離或分佈來概括。由此產生了一個具有深遠意義的觀點：這條曲線標明了不確定的區域。我們不能肯定曲線的中心是否就是那確鑿無誤的位置。我們只能說：“它位於不確定的區域”，而這個位置可以根據個別觀察中所得出的分佈情況計算出來。

植物器官表面彎曲的研究應用

植物器官表面彎曲程度可以用高斯曲線表示，以互相垂直方式產生曲線。一般的葉面是扁平的，而沒有缺口或摺疊，說明了近似零的高斯曲率，平面的勻質生長，例如相同膨脹的盤，保持零的高斯曲線，如果邊緣區域生長比中心生長緩慢，這個盤子會趨於杯狀具備正的高斯曲線，如果邊緣區域生長更快，這個盤子將彎曲變形成一個波浪邊，例如鞍狀，為負的高斯曲線。曲率受到遺傳控制。