曲率

弧的切線轉角與該弧長之比的絕對值稱作該弧的平均曲率，記作

當沿曲線L趨向於M時，若弧的平均曲率的極限存在，則稱此極限為曲線L在點M處的曲率，記作K，即或。

設曲線的直接坐標方程為，且具有二階導數，曲線在點M處的切線的斜率為,所以

又,故曲線L在M點處的曲率為

設曲線是由參數方程給出，利用參數方程求導法可得

曲線上點M處的曲率的倒數，稱作曲線在這點處的曲率半徑，記作,則

在點M處曲線的法線的某一側上取一點D，使，並以D為圓心，以為半徑作圓。把這個圓稱作曲線在M處的曲率圓，把圓心D稱做曲線在M處的曲率中心。

曲率圓具有以下性質：

（1）曲率圓與曲線在點M處有共同的切線和曲率；

（2）在點M鄰近與曲線有相同的凹向；

因此，在實際工程設計問題中，常用曲率圓在點M鄰近的一段圓弧來近似代替曲線弧，以使問題簡化。

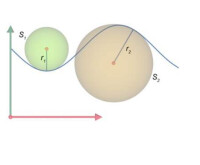
曲率是幾何體不平坦程度的一種衡量。平坦對不同的幾何體有不同的意義。

本文考慮基本的情況，歐幾里得空間中的曲線和曲面的曲率。一般意義下的曲率，請參照曲率張量。

在動力學中，一般的，一個物體相對於另一個物體做變速運動時也會產生曲率。這是關於時空扭曲造成的。結合廣義相對論的等效原理，變速運動的物體可以看成處於引力場當中，因而產生曲率。

按照廣義相對論的解釋，在引力場中，時空的性質是由物體的“質量”分佈決定的，物體“質量”的分佈狀況使時空性質變得不均勻，引起了時空的彎曲。因為一個物體有質量就會對時空造成彎曲，而你可以認為有了速度，有質量的物體變得更重了，時空彎曲的曲率就更大了。

在物理中，曲率通常通過法向加速度（向心加速度）來求，具體請參見法向加速度。