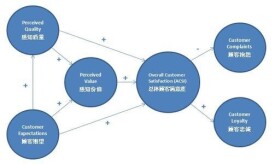
潛在變數
潛在變數
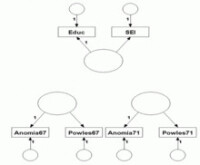
潛在變數
(1)、和一個結構方程模型:η=Bη+ΓX+ζ
(2)、其中X、ξ表示外生的(原因)顯在變數和潛在變數,Y、η表示內生的(結果)顯在變數和潛在變數。關於上述模型的詳細假設可參考相關文獻。
人們在應用上述模型解決實際問題時常有這樣的體會:一個突出的問題是變數間的線性關係假設使得某些實際資料擬合結果不太符合專業知識,本文擬在變數間非線性關係假設下,就如何建模、尋求參數估計等理論做了探討,從而提高了原來線性假設下LISREL擬合實際問題的準確性。
2、變數變換及其似然函數設有一外生可觀測向量Z(P×1)經函數f(.)變換后成X(P×1),且假定X服從正態分佈Np(μ,∑(θ)),θ為模型中的待估計參數族,則模型可定義為X=f(Z),ξ=B0ξ+ζ,X=μ+Aξ+ε。
(3)、假設隨機向量ξ、ζ和ε的期望為零,且互不相關,X的期望為μ,易求得X的協方差陣為∑(θ)=∧B-1ΦB-T∧T+Ψ。
(4)、其中,B=IΓ-B0,Φ=cov(ξ),Ψ=cov(ε),B-T是B的轉置的逆矩陣,我們的目的是由此導出X的似然函數。
由X~Np(μ,∑(θ))可寫出X的密度函數。
第一步,用一般的LISERL方法擬合原始資料,若發現某些線性假設下的估計結論與理論不符,則進入下一步;
第二步,對上步中不符的線性假設下聯繫的變數做變換(一般做Box-Cox變換),使其近似服從正態分佈,並進入下一步;
第三步,對變換后的資料擬合LISREL模型;
第四步,對最終擬合結果做出專業解釋。