極限尺寸
允許零件尺寸變化的界限值
極限尺寸是指允許零件尺寸變化的兩個界限值。較大的一個稱為最大極限尺寸;較小的一個稱為最小極限尺寸。極限尺寸是在設計確定基本尺寸的同時,考慮加工的經濟性並滿足某種使用上的要求確定的。
1905年,美國人W.泰勒(William Taylor)提出“螺紋量規改進”這一專利。
通端量規由三個測頭b組成,經過通端量規檢驗合格的螺紋,還需要進行止端檢驗。止端檢驗的方法是先將下側測頭b與外螺紋的小徑接觸,然後觀察測量銷c'是否能塞進量規與上側平面c與外螺紋小徑之間的空隙,如果塞不進去,則螺紋為合格。
從符合泰勒原則的檢驗方法可以看出,其最大實體尺寸是MMC邊界尺寸,由極限量規的通端控制,理論上“通規”是長度等於被測要素結合長度的完全圓柱表面(全形量規)。最小實體尺寸是局部實際尺寸,由極限量規的止端控制,“止規”是具有量面為兩點狀的表面(非全形量規)。
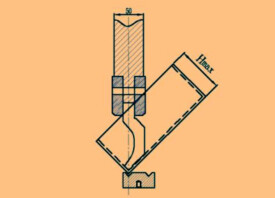
採用最大實體原則以後,如把最大實體尺寸解釋為MMC邊界尺寸,生產上將會引起混亂。如圖2所示,銷軸在最大實體狀態時還允許有t的直線度誤差,實效尺寸為,綜合量規如圖2所示。已如前述,凡被綜合量規接受的零件均能保證裝配互換性。但是按泰勒原則設計的“通規”來檢驗尺寸公差時,一定會拒收作用尺寸大於d而小於 的零件。由此可見,有一部分能被綜合量規接收,可以滿足裝配互換性的零件,有一部分會被極限量規拒收作為廢品,這顯然是不合理的,也是極不經濟的。所以採用最大實體原則時,把最大實體尺寸解釋為MMC邊界尺寸是錯誤的。應該和最小實體尺寸一樣解釋為局部實際尺寸,採用兩點測量法進行檢驗才是合理的。
獨立原則不考慮尺寸公差與形位公差的相互依賴關係,因此必須用不控制實際形狀的兩點測量法檢驗尺寸。此時最大實體尺寸和最小實體尺寸都應該解釋為局部實際尺寸,這樣才能保證獨立原則的應用。
極限尺寸的判斷原則(即泰勒原則):
孔或軸的作用尺寸不允許超過最大實體尺寸。即對於孔,其作用尺寸應不小於最小極限尺寸;對於軸,則應不大於最大極限尺寸。
在任何位置上的實際尺寸不允許超過最小實體尺寸,即對於孔,其實際尺寸應不大於最大極限尺寸;對於軸,則應不小於最小極限尺寸。
在孔的極限尺寸中,例如,形狀誤差可能的極端情況;
在軸的極限尺寸中,例如,形狀誤差可能的極端情況。
與使用性能或裝配精度要求有關的極限尺寸常採用以下幾種注法:
● ● 直接注出最大和最小極限尺寸注出極限尺寸后,可不用任何說明。
2.控制尺寸數值在某一尺寸之下
除注出尺寸數值外,還需附以文字註解。
3.只注出最大或最小極限尺寸
在彈簧裝配中,由於彈簧有內、外表面定位的區別,通常需要在彈簧零件圖上控制其內、外徑的極限尺寸,以保證其可靠裝配。
為了方便慣性簧3在滑座1孔內裝配,要求慣性簧的外徑略小於滑座孔的孔徑,這時只要控制慣性簧外徑的最大極限尺寸即可。