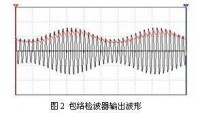
包絡
用於數學、經濟學領域的幾何學
在數學上,一族平面直線(或曲線)的“包絡”(envelope)是指一條與這族直線(或曲線)中任意一條都相切的曲線。假設這族平面曲線記為,這裡不同的t 對應著曲線族中不同的曲線,則包絡線上的每一點滿足右下端的兩條方程,由這兩條方程消去t后便可得出包絡線的隱式表示。
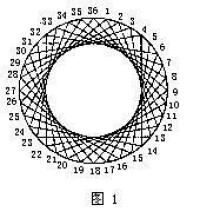
包絡線
如圖1中的直線組成一個圈,然而實際上我們並沒有“畫”這個圓,這時就把這個圓稱作是包絡線。
要想畫出類似的包絡線,首先要畫出一個大圓(例如直徑10cm),並把圓周分成36等分,用量角器每10°作一點即可。
把第n點與第點連線,就可畫出圓形包絡線。如果大於36,則須減去36。例如當時,,減去36之後得到3,所以第29點是與第3點連線。
我們可以將任一平穩窄帶實高斯隨機過程X(t)表示為準正態振蕩的形式:
其中是窄帶隨機過程的載波頻率;和是的包絡和相位。包絡即隨機過程的振幅隨著時間變化的曲線。
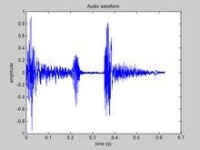
QQ系統提示音的時間振幅圖像
它的內容是考慮含參量a的函數的無條件極值問題(x是內生變數,a是外生變數)。顯然,一般地其最優解V是參量a的函數,即。
包絡定理指出:V對a的導數等於f對a的偏導數(注意是f對“a所在位”變數的偏導數)。
1、意為包圍環繞。

《徐霞客遊記》
2、意為猶包括。