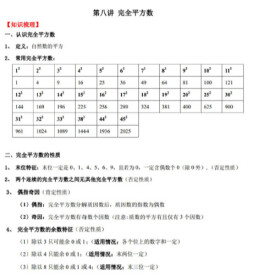
完全平方數

整  某整  ，整  完。零稱完。質：

（）平方數的個位數字只能是 0， 1，4，5，6，9 。

（）偶  整除；奇 ( )除余 ，即 除余    完。

（3）完全平方數的個位數字是奇數時，其十位上的數字必為偶數。完全平方數的個位數字是 6 時，其十位數字必為奇數。

（4）凡個位數字是 5 但末兩位數字不是 25 的自然數不是完全平方數；末尾只有奇數個 0 的自然數不是完全平方數；個位數字是 1，4，9 而十位數字為奇數的自然數不是完全平方數。

（5）除 1 外，一個完全平方數分解質因數后，各個質因數的指數都是偶數，如果一個數質分解后，各個指數都為偶數，那麼它肯定是個平方數。完全平方數的所有因數的總個數是奇數個。因數個數為奇數的自然數一定是完全平方數。

（6）若質數 p 整除完全平方數 a，則。

（7）如果 a 、b 是平方數， ，那麼 c 也是完全平方數。

（8）兩個連續自然數的乘積一定不是平方數，兩個連續自然數的平方數之間不再有平方數。

（9）如果十位數字是奇數，則它的個位數字一定是6；反之也成立。

推論1：如果一個數的十位數字是奇數，而個位數字不是6，那麼這個數一定不是完全平方數。

推論2：如果一個完全平方數的個位數字不是6，則它的十位數字是偶數。

（10）偶數的平方是4的倍數；奇數的平方是4的倍數加1。

（11）奇數的平方是型；偶數的平方為或型。（奇數：n比那個所乘的數；偶數：n比那個所乘的數）

（12）形式必為下列兩種之一：。

（13）不是5的因數或倍數的數的平方為型，是5的因數或倍數的數為5k型。

（14）形式具有下列形式之一：。

（15）性質11：如果質數p能整除a，但p的平方不能整除a，則a不是完全平方數。

（16）在兩個相鄰的整數的平方數之間的所有整數都不是完全平方數。

（17）一個正整數n是完全平方數的充分必要條件是n有奇數個因數（包括1和n本身）。

（1）個位數是2、3、7、8的整數一定不是完全平方數；

（2）個位數和十位數都是奇數的整數一定不是完全平方數；

（3）個位數是6，十位數是偶數的整數一定不是完全平方數；

（4）形如型的整數一定不是完全平方數；

（5）形如和型的整數一定不是完全平方數；

（6）形如型的整數一定不是完全平方數；

（7）形如型的整數一定不是完全平方數；

（8）數字和是2、3、5、6、8的整數一定不是完全平方數；

（9）四平方和定理：每個正整數均可表示為4個整數的平方和；

（10）完全平方數的因數個數一定是奇數。

完全平方式分兩種：

（1）完全平方和公式，就是兩個整式的和括弧外的平方，例如：

（2）完全平方差公式，就是兩個整式的差括弧外的平方。例如：

口訣：首末兩項算平方，首末項乘積的2倍中間放，符號隨中央。（就是把兩項的乘方分別算出來，再算出兩項的乘積，再乘以2，然後把這個數放在兩數的乘方的中間，這個數以前一個數間的符號隨原式中間的符號，完全平方和公式就用+，完全平方差公式就用，後邊的符號都用）

一個數如果是另一個整數的完全平方，那麼我們就稱這個數為完全平方數，也叫做平方數。

它與完全平方式的區別是：完全平方式是代數式，完全平方數是自然數。

一個自然數減去45及加上44都仍是完全平方數，求此數。

解：設此自然數為x，依題意可得：

⑴

⑵

（m,n為自然數）

⑵-⑴可得：

因為

又因為89為質數，

所以：

解之，得。代入⑵得。故所求的自然數是1981。

● ● （1986年第27屆IMO試題） 設正整數d不等於2,5,13，求證在集合中可以找到兩個不同的元素a,b，使得不是完全平方數。解：顯然都為完全平方數.假設為完全平方數,注意到d為正整數,為奇數 不妨設得.此時不是完全平方數.同理 假設為完全平方數可以分d為奇偶去證明.

● ● 求k的最大值，使2010可以表示為k個連續正整數之和。解：假設這k個數為 .它們的和為,,顯然k最大隻能是60,此時