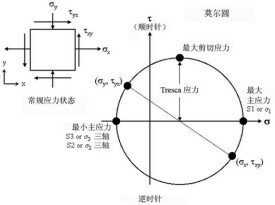
莫爾圓
K.庫爾曼、O.莫爾提出的理論
莫爾圓在應力(或應變)坐標圖上表示受力(或變形)物體內一點中各截面上應力(或應變)分量之間關係的圓。表示應力的稱為應力莫爾圓;表示應變的稱為應變莫爾圓。
對於二嚮應力狀態,若已知如圖1所示的單元體(實際代表物體中一個點)在兩相互垂直的截面上的應力、和、(其中和為正應力,以拉伸為正;和為剪應力,順時針為正,且=-)則在以正應力為橫坐標、剪應力為縱坐標的坐標系中,可按下述步驟畫出莫爾圓:根據已知應力分量在坐標系中畫出(,)和(,)兩點,以連線與軸的交點C為圓心,以(或)為半徑畫圖,即得莫爾圓。莫爾圓的方程是:
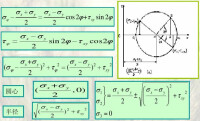
圖3莫爾圓
二嚮應力狀態的莫爾圓有如下性質:
①莫爾圓上每一點的坐標都對應於單元體上某一截面上的正應力和剪應力;
②若莫爾圓上的兩個點組成的圓心角為,則單元體上相應的兩個截面的外法向的夾角為α,且角度的轉向相同。
根據上述性質,以單元體上某個面為基面,以莫爾圓上與該面對應的點為基點,就能求出單元體中各截面上的應力,或找出最大剪應力面和主平面(即剪應力為零的平面)的方向。
三嚮應力狀態的莫爾圓是在已知物體上一點的三個主應力的前提下得到的。如圖4所示,若,則三嚮應力狀態的莫爾圓具有如下性質:物體內所考慮點的任意方向截面上的正應力和剪應力在坐標系中對應的點,都落在圖中的陰影部分。即莫爾圓給出了一點的應力範圍。若已知截面的法向與三個主應力方向的夾角或方向餘弦,也可通過幾何方法確定出該截面上正應力和剪應力的值。但在一般工程應用中,知道應力範圍就足夠了。對於應變,也有相同形式的莫爾圓。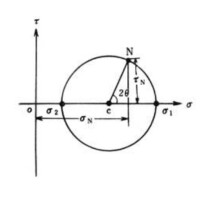

圖4莫爾圓
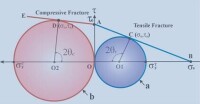
莫爾圓
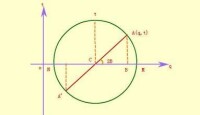
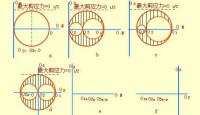
以平面應力為例說明二維應力莫爾圓的性質:受力物體內某一截面上的正應力和剪應力都是該截面法線與最大主應力夾角的函數,可以分別用公式表示為式中和為兩個主應力。這兩個關係式也可以用莫爾圓上點的坐標值(見圖)來表示,點與夾圓心角為。當(和為已知時,用公式法或莫爾圓法都可獲得通過該點的任一截面上的正應力和剪應力值。莫爾圓法的操作是:取為橫坐標,為縱坐標,在橫坐標上分別取量值為,的兩點,取兩點間的中點為圓心作圓,則此圓的圓心坐標為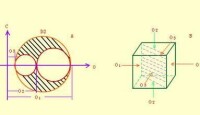 圓半徑值為如果欲知道法線與夾角為的截面上的正應力和剪應力,可從開始,量得圓心角為而獲得點,則點的橫坐標恰好為該截面上的正應力值,點的縱坐標恰好為該截面的剪應力值。點的橫坐標值等於圓心的橫坐標值加上半徑值與之積,即與公式的結果一樣;點的縱坐標值等於半徑值與之積,即與公式的結果也一樣。改變角就可以獲得任意截面上的正應力與剪應力值。當或時,其最大的縱坐標值即它表示法線與最大主應力分別夾45°和135°的截面上剪應力最大,但兩者有相反的符號。當或者,恰好是和兩點,這兩點的縱坐標值為零,表示主應力作用面上沒有剪應力,而且與之間夾角,即彼此永遠垂直。
圓半徑值為如果欲知道法線與夾角為的截面上的正應力和剪應力,可從開始,量得圓心角為而獲得點,則點的橫坐標恰好為該截面上的正應力值,點的縱坐標恰好為該截面的剪應力值。點的橫坐標值等於圓心的橫坐標值加上半徑值與之積,即與公式的結果一樣;點的縱坐標值等於半徑值與之積,即與公式的結果也一樣。改變角就可以獲得任意截面上的正應力與剪應力值。當或時,其最大的縱坐標值即它表示法線與最大主應力分別夾45°和135°的截面上剪應力最大,但兩者有相反的符號。當或者,恰好是和兩點,這兩點的縱坐標值為零,表示主應力作用面上沒有剪應力,而且與之間夾角,即彼此永遠垂直。

莫爾圓
莫爾圓
莫爾圓