光學傳遞函數

觀察各類，儀器（照、鏡、顯微鏡）系統、探測圖標，荷耦合器件（）、數碼相機和計算機多媒體獲得的圖形、圖像，具有顏色和亮度兩個重要的參數。限於考慮二維的非相干單色光平面圖像，則圖像的光強分佈就成為描繪、規定該圖像的主要參數。一幅單色光圖像總是由緩慢變化的背景、粗大的物體和急劇變化的邊緣、局部細節構成。傅里葉光學中用空間頻率 ν來描述光強空間變化的快慢程度，把圖像中緩慢變化的成分看作圖像的“低頻”，而把急劇變化的成分看作圖像的“高頻”，單位是“1/毫米”，即每毫米中光強變化的周期數。空間頻率等於0表明圖像中沒有光強變化（如一張白紙）。一幅圖像中既有零頻分量，又有非零頻分量，後者包含了各種空間頻率的分量。零頻分量代表平均光強，稱圖像的直流分量；非零頻分量又稱圖像的交流分量。光學成像系統對於各種空間頻率成分的傳遞性能反映了該系統的成像質量，可藉助於系統對於不同空間頻率餘弦光柵的傳遞特性來表徵。

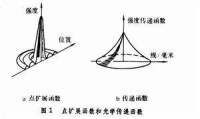
置系統輸、空頻率 ν的一維餘弦光柵的光強分佈可表為：

系統強布則：

式中 m( ν)為調製度或反差度，代表交流分量的幅度與直流分量的比。輸入餘弦 光柵的調製度為1，為滿幅調製； ，等號僅當時才成立。 m( ν)表徵系統對於空間頻率為 ν的餘弦信號的調製度的衰減，稱為調製傳遞函數； φ( ν)則表示餘弦光柵亮條紋的位置向暗條紋位置的相對移動，稱為相位傳遞函數。複函數：

稱為光學傳遞函數。調製傳遞函數是光學傳遞函數的模，歸一化手續規定，說明任何成像系統對於均勻一致的亮場（零頻）總會響應。緩慢變化的背景和粗大物體通過系統形成像比較清晰，系統的低頻調製傳遞函數比較高。空間頻率越高，調製傳遞函數越小，表明越細微的物體光學系統的解析度越低，那些的物體細節會在通過系統的像強度分佈中變得非常模糊乃至消失。調製傳遞函數 m( ν)全面反映了從低頻到高頻的分量的傳遞特性，是評價系統成像質量的主要指標。許多場合下光學傳遞函數指的就是調製傳遞函數。若干成像系統串聯時，合成系統的光學傳遞函數是子系統光學傳遞函數的乘積。

光學系統只有有限的孔徑，空間頻率過高時餘弦光柵的衍射光離軸角過大，不能進入系統，因此存在截止頻率（極限頻率） 對於非相干成像系統，

式中 F為成像系統的 F數（焦距/孔徑）， λ為光波波長，N.A.為數值孔徑。超過截止頻率的圖像細節將不能通過系統。為此，光學系統是低頻濾波器。相同規格（如 F數相同）的成像系統具有相同的截止頻率。

評價大視場光學系統的成像質量時，不但要考慮低頻、中頻和高頻的調製傳遞函數（MTF）的大小，還要全面評價對應於不同視場的一系列傳遞函數曲線。軸外視場對於水平方向（子午方向）放置的餘弦光柵和垂直方向（弧矢方向）放置光柵的調製傳遞函數並不相同，所以要同時考察子午MTF和弧矢MTF。一般說來，調製傳遞函數曲線整體越高，系統的成像質量越好。在某些應用中還需要考慮相位傳遞函數。但在普通成像鏡頭生產線上，為了快速高效判別成像質量，可用幾個甚至一個空間頻率的調製傳遞函數 m( ν)與閾值的比較來作為鏡頭像質是否合格的判據，產業部門這樣的近似已經夠用。 又稱特徵頻率，通常取 。

為了得到點光的像強度分佈，必須考慮衍射效應，才能對物和像之間關係有更全面理解。根 據光的衍射理論可以研究點光源至透鏡、至像平面光波的整個傳播過程，最後得出像平面上強度分佈是透鏡孔徑函數的夫琅和費衍射圖樣，稱為光學系統的強度脈衝響應，或點擴展函數。由它可以確定光學系統的成像性質，因為任意複雜物體由無數點源組成，其像的強度為物強度與點擴展函數的卷積。圖1a表示一個無像差理想光學成像系統的點擴展函數。

利用點擴展函數概念可對光學系統的解析度作出判據，例如對於兩個點源組成的物，在像平面上的強度分佈是相應兩點擴展函數的疊加。當兩點源距離小於點擴展函數的半寬度即點擴展函數第一零點的半徑時，兩點源在像平面上不能分辨。

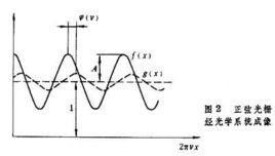
與研究電學系統相似，引入傅里葉分析方法，考慮輸入各種不同空間頻率的物函數，觀察光學系統像面上輸出情況，例如物是餘弦形式的光柵。因光學系統是線性的，所以像強度分佈也是餘弦形式，但它的振幅和位相會受系統的影響。正弦光柵經光學系統成像后，比原物相比反襯度降低，最高強度降低，最低強度升高，設 T( v)滿足。另外還會產生相移。原來亮線條的位置會向暗線條方向移動。 T( v)是空間頻率 v的函數，改變 v可測得 T( v)隨 v變化曲線，反映系統對各空間頻率的傳遞情況。對 即零空間頻率的圖像信息，在系統中傳遞不受損失；而對那些 的圖像頻率成分，會在像強度分佈中消失。一般地， T( v)是複數，此時傳遞函數是實函數。

點擴展函數是一點光源經光學系統后所成的衍射斑分佈的函數。它在空域表徵光學系統的特性，傳遞函數在頻域表徵系統的特性。實際上兩者有簡單關係，即點擴展函數的傅里葉變換就是光學系統的傳遞函數。點擴展函數與透鏡的孔徑函數有關，傳遞函數也與孔徑函數有關。事實上傳遞函數是孔徑函數的自相關函數。

一個光學系統質量的評價，早期採用“星點”法，即觀察點光源的像的強度分佈，實質上是把對點擴展函數形狀的觀察作為像質評價的判據。這種方法雖然直觀，但帶有主觀性，不能作定量評價。現在人們廣泛用傳遞函數作為像質評價的判據，使質量評價進入客觀計量。