多目標決策
多目標決策
系統方案的選擇取決於多個目標的滿足程度,這類決策問題稱為多目標決策,或稱為多目標最優化。
目錄
當決策對象具有多個評價目標時,從若干可行方案(也稱解)中,選擇一個滿意方案(解)的決策方法。進行多目標決策時,根據事前確定的評價標準,從一組非劣解中,通過“辨優”和“權衡”找出一個令人滿意的解。
發展簡況 多目標最優化問題最早是由義大利經濟學家L.帕雷托在1896年提出來的,他把許多本質上是不可比較的目標化成一個單一的最優化目標。1944年J.von諾伊曼和O.莫根施特恩又從對策論角度提出具有多個決策者並相互矛盾的多目標決策問題。1951年T.C.考普曼從生產和分配活動分析中提出多目標最優化問題,並引入了帕雷托優化的概念。1961年A.查納斯和W.庫珀提出目標規劃。1963年L.A.瑞特從控制論角度提出多指標問題的一些基本概念。1976年R.基奈和H.拉伊發利用多屬性效用方法求解多目標問題。60年代以來,出現了很多解決多目標決策問題的方法。中國70年代中期開始推廣應用多目標決策方法,現在已取得了一定的成果。
數學模型 多目標決策問題的某一可行方案與其他可行方案兩兩比較時,其結果有三種可能:①所有目標都是最優的方案,稱為完全最優解,這種情況極少出現。②所有目標都是最劣的方案,稱為劣解,立即可以淘汰。③目標有優有劣,既不能肯定方案為最優,也不能立即予以淘汰,這種方案稱為非劣解,又稱有效解或帕雷托最優解。多目標最優問題的數學模型為:設系統有 m個目標f1(x),f2(x),…,fm(x),要求評價由n個變數組成的方案x=(x1,x2,…,xn)T,如果這些目標都要求最大(或最小),並要求解滿足約束條件集合R,則數學模型可表達成如下形式:
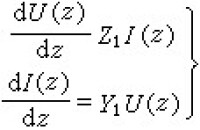
多目標決策
式中F(x)=(f1(x),f2(x),…,fm(x))為目標向量。
多目標決策方法 多目標決策主要有以下幾種方法:①化多為少法:將多目標問題化成只有1個或2個目標的問題,然後用簡單的決策方法求解,最常用的是線性加權和法。②分層序列法:將所有目標按其重要程度依次排序,先求出第一個(最重要的)目標的最優解,然後在保證前一目標最優解的前提下依次求下一目標的最優解,一直求到最後一個目標為止。③直接求非劣解法:先求出一組非劣解,然後按事先確定好的評價標準從中找出一個滿意的解。④目標規劃法:當所有目標函數和約束條件都是線性時,可以採用目標規劃法。它是60年代初由查納斯和庫珀提出來的。對每一個目標函數都事前給定一個期望值,然後在滿足約束條件集合的情況下,找出使目標函數離期望值最近的解。⑤多屬性效用法(MAUM):各個目標分別用各自的效用函數表示,然後構成多目標綜合效用函數,以此來評價各個可行方案的優劣。⑥層次分析法:它是由T.沙基於1980年提出來。這種方法是通過對目標、約束條件、方案等的主觀判斷,對各方案加以綜合權衡比較,然後評定優劣。⑦重排次序法:把原來不好比較的非劣解通過其他辦法使其排出優劣次序來。此外,還有多目標群決策和多目標模糊決策等方法。
線性加權和法 化多為少法的一種常用方法。對m個目標fi(x)分別給以權係數λi(i=1,2,…,m),然後作新的目標函數(又稱效用函數):要求它越大越好。即對原來求向量極值的問題 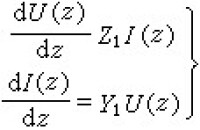 改為求標量極值。求解新的目標函數前,先將具有不同量綱的目標值用同一尺度統一起來。一般用效用值予以統一。另一問題就是合理選擇各個目標函數的權係數。
改為求標量極值。求解新的目標函數前,先將具有不同量綱的目標值用同一尺度統一起來。一般用效用值予以統一。另一問題就是合理選擇各個目標函數的權係數。
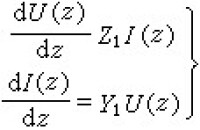
多目標決策
平方和加權法 化多為少法的一種。設有規定的m個值為,要求m個函數f1(x),f2(x),…,fm(x),分別與規定的值相差程度盡量小,這時採用評價函數:,要求。其中λi可按不同要求相差程度分別給出。
序列最優化法 分層序列法一種。將m個目標按重要程度依次排序為f1(x),f2(x),…,fm(x),先對第一個目標求最優,並找出所有最優解的集合R0;然後在R0內求第二個目標的最優解,找出最優解的集合R1;如此類推,直到求出m個目標的最優解及其集合Rm-1為止,其模型為:
…,
多目標決策
這種方法有解的前提是R0,R1,…,Rm-1都是非空集合,且R0,R1,…,Rm-2都不止有一個元素。序列最優化法用於工程設計的情況下,在求后一個目標最優時前一個目標不必達到嚴格最優,只要在一定範圍內(例如在一定公差範圍內)即可,這樣就變成求一系列帶有寬容條件的極值問題,稱為允許寬容的序列最優化。其模型為
……
其中a1,…,ɑm-1為給定的寬容限值。
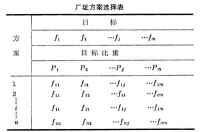
重排次序法 以厄勒克特拉法為代表。現舉廠址選擇為例,設有m個目標和n個備選方案,fj(j=1,2,…,m)為造價、運輸費、燃料費、施工期限以及其他社會政治因素等各種目標,Pi為相應的目標比重,fij(i=1,2,…,n;j=1,2,…,m)為第i個方案第j個目標fj的取值(見表)。
多目標決策
多目標決策
多目標決策
多目標決策
多目標決策
參考書目
C.L.Hwang and A.S.M.Masud, Multiple Objective Decision Making-Methods and Applications, A State-of-the-Art Survey,Springer-Verlag, Berlin,1979.
C.L.Hwang and K. Yoon, Multiple Attribute Decision Making-Methods and Applications, A State-of-the-Art survey Springer-Verlag,Berlin,1981.