頻譜泄露
頻譜泄露
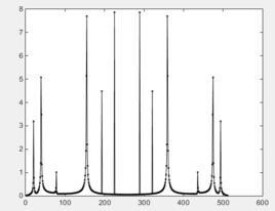
對於頻率為fs的正弦序列,它的頻譜應該只是在fs處有離散譜。但是,在利用DFT求它的頻譜時,對時域做了截斷,結果使信號的頻譜不只是在fs處有離散譜,而是在以fs為中心的頻帶範圍內都有譜線出現,它們可以理解為是從fs頻率上“泄漏”出去的,這種現象稱 為頻譜“泄漏”。
目錄
在實際問題中遇到的離散時間序列x(n)通常是無限長序列,因而處理這個序列的時候需要將它截短。截短相當於將序列乘以窗函數w(n)。根據頻域卷積定理,時域中x(n)和w(n)相乘對應於頻域中它們的離散傅立葉變換X(jw)和W(jw)的卷積。
因此,x(n)截短后的頻譜不同於它以前的頻譜。
小說幾句。時域上乘上窗函數,相當於頻域進行卷積。長度為無窮長的常數窗函數,頻域為delta函數,卷積后的結果和原來一樣。如果是有限矩形窗,頻域是Sa函數,旁瓣電平起伏大,和原頻譜卷積完,會產生較大的失真。
窗的頻譜,越像delta函數(主瓣越窄,旁瓣越小),頻譜的還原度越高。於是,就產生了那麼多bt的窗函數。
加窗就不可避免頻譜泄漏,典型的加權序列有Hamming、Blackman、Gaussian等窗序列主要是為了降低旁瓣,對於降低頻譜泄漏效果遠不如增加窗序列的長度明顯吧。
周期信號加窗后做DFT仍然有可能引起頻譜泄露,設fs為採樣頻率,N為採樣序列長度,分析頻率為:m*fs/N(m=0,1....),以cos函數為例,設其頻率為f0,如果 f0不等於m*fs/N,就會引起除f0以外的其他m*fs/N點為非零值,即出現了泄露。
DFT作為有限長的運算,對於無限長的信號必須要進行一定程度的截斷,既然信號已經不完整了,那麼截斷後的信號頻譜肯定就會發生畸變,截斷由窗函數來完成,實際的窗函數都存在著不同幅度的旁瓣,所以在卷積時,除了離散點的頻率上有幅度分量外,在相鄰的兩個頻率點之間也有不同程度的幅度,這些應該就是截斷函數旁瓣所造成的。