斷裂力學

cfsaghyrjkhk固體力學的一個新分支。研究帶有初始裂紋的構件發生低應力脆斷的規律性，並據此提供防止這種斷裂的計算方法。低應力脆斷是構件在承受的拉應力遠低於材料的屈服強度時所發生的意外斷裂，是裂紋從裂紋源處擴展到全斷面而造成的。

斷裂力學中對於材料所用的力學模型比材料力學中的力學模型多一條或幾條裂紋，也就是說，材料為均勻、連續介質的假設仍被引用，只是在個別有裂紋的部位，介質的連續性才被破壞。

在研究裂紋處有拉應力的構件（如帶初始裂紋的拉伸或彎曲構件）的低應力脆斷規律時，除了裂尖附近的極微小區域外，材料均處於線彈性狀態，故可按線彈性力學的方法對裂尖附近區域內的應力、應變和位移進行分析。由於裂紋的力學模型是在尖端處曲率半徑等於零的尖切口，因此，按線彈性力學方法求得的裂尖處的應力就具有奇異性，而這種應力奇異性的強度通常被稱為裂尖處的應力強度因子，用KI表示(見圖)。 KI值與拉伸或彎曲構件在裂尖位置處的拉應力σ 成正比，並與裂紋尺寸參數a的平方根成正比。線彈性斷裂力學認為，帶裂紋構件裂紋發生失穩擴展的必要條件是：裂尖處的應力強度因子KI達到材料的臨界應力強度因子值KIc。KIc通常稱為材料的平面應變斷裂韌度，其值可通過對於帶有初始裂紋的拉伸或彎曲試樣進行試驗求得。當試樣尺寸符合一定的要求時，用試樣測得的斷裂韌度KIc值就與試樣的幾何尺寸及它們之間的比例無關，而是材料固有的力學性能。對於各種受力情況及裂紋情況下的構件，在裂尖處的應力強度因子目前已有手冊備查，常用材料的斷裂韌度KIc值也有試驗數據可查。因此，按線彈性斷裂力學方法，就可以評定帶初始裂紋的構件對於低應力脆斷的安全性，以此作為常規強度計算的一個補充。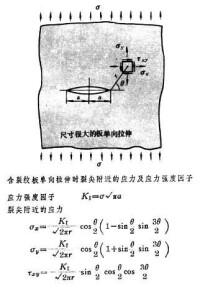很多帶初始裂紋的構件是用低強度、高韌度材料製成的。在裂紋發生失穩擴展前，裂紋尖端附近已出現了較大範圍的塑性區。對這類構件，線彈性斷裂力學的分析方法已不適用。按彈塑性斷裂力學的觀點來判斷這種裂紋起始擴展的條件，通常是以裂紋尖端處的張開位移值δ達到裂紋開裂時材料的臨界值δcr作為判據。也有時採用在裂紋周圍彈塑性區域內一個與積分線路無關的能量線積分 J達到裂紋啟裂時材料的臨界值JIc作為判據。J和δ這兩個參數在線彈性條件下均與應力強度因子KI存在著確定的關係。材料的這兩個固有的力學性能δcr和JIc可稱為材料在彈塑性條件下的斷裂韌度值。由於在彈塑性範圍內裂紋從啟裂到失穩擴展這一過程中，構件的承載能力還有所增長，所以，按啟裂時的δcr或JIc進行計算是偏於保守的。

近年來，已開始將斷裂力學中的參量，例如K、J、δ等，用來描述帶裂紋構件在疲勞、蠕變、應力腐蝕等過程中裂紋擴展的規律，據此判定這類構件的使用壽命。這方面的研究已取得了初步的成功，並在飛機結構、反應堆壓力容器及管道等方面應用。但對擴展中的裂紋，當其裂紋擴展量較大時，為描述裂紋尖端處的應力、應變及位移場，需用一個新的參量來代替原來常用的K、J、δ等參量才更恰當。對此還有大量的理論和實驗工作有待進行。

參考書目

D.布洛克著，王克仁等譯：《工程斷裂力學基礎》，科學出版社，北京，1980。(D.Brock，Elementary Enɡineerinɡ Fracture Mechanics，Noordhoff,Leyden，1974.)