倒圓錐體
倒圓錐體
圓錐也稱為圓錐體,是一種三維幾何體,是平面上一個圓以及它的所有切線和平面外的一個定點確定的平面圍成的形體。圓形被稱為圓錐的底面,平面外的定點稱為圓錐的頂點或尖端,頂點到底面所在平面的距離稱為圓錐的高。通常“圓錐”一詞用來指代正圓錐,也就是圓錐頂點在底面的投影是圓心時的情況。正圓錐可以定義為一個直角三角形繞其中一條直角邊旋轉一周得到的幾何體,這個直角三角形的斜邊稱為圓錐的母線。頂點在底面的投影不在圓心,這樣的圓錐稱為斜圓錐。正圓錐可以由平面截圓錐面得到,斜圓錐則不能。傾斜平面截取圓錐面得到的幾何形體叫做橢圓錐。
圓錐的高:圓錐的頂點到圓錐的底面圓心之間的距離叫做圓錐的高;
圓錐母線:圓錐的側面展開形成的扇形的半徑、底面圓周上任意一點到頂點的距離。
圓錐的側面積:將圓錐的側面沿母線展開,是一個扇形,這個扇形的弧長等於圓錐底面的周長,而扇形的半徑等於圓錐的母線的長. 圓錐的側面積就是弧長為圓錐底面的周長×母線/2;沒展開時是一個曲面。
圓錐有一個底面、一個側面、一個頂點、一條高、無數條母線,且底面展開圖為一圓形側面展開圖是扇形。
圓錐是一種幾何圖形,有兩種定義。解析幾何定義:圓錐面和一個截它的平面(滿足交線為圓)組成的空間幾何圖形叫圓錐。立體幾何定義:以直角三角形的直角邊所在直線為旋轉軸,其餘兩邊旋轉360度而成的曲面所圍成的幾何體叫做圓錐。旋轉軸叫做圓錐的軸。垂直於軸的邊旋轉而成的曲面叫做圓錐的底面。不垂直於軸的邊旋轉而成的曲面叫做圓錐的側面。無論旋轉到什麼位置,不垂直於軸的邊都叫做圓錐的母線。(邊是指直角三角形兩個旋轉邊)
體積公式
底面積×高×1/3 V錐=1/3sh
表面積公式
側面積+底面積 πLR+πr²
圓錐三視圖是觀測者從三個不同位置觀察而畫出的圖形。
其主視圖和側視圖均為等腰三角形,俯視圖是一個圓和圓心。
圓錐體展開圖由一個扇形(圓錐的側面)和一個圓(圓錐的底面)組成。(如右圖)
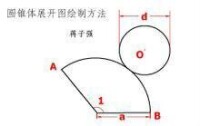
繪製方法
∵弧AB=⊙O的周長
∴弧AB=πd
∵弧AB=2πa(∠1/360°)
∴2πa(∠1/360°)=πd
∴2a(∠1/360°)=d
將a,d帶入2a(∠1/360°)=d得到∠1的值。這樣繪製展開圖的所有所需數據都求出來了。根據數據即可畫出圓錐的展開圖。
母線長等於底面圓直徑的圓錐,展開的扇形就是半圓。所有圓錐展開的扇形角度等於(底面直徑÷母線)×180度。
| 圓錐的計算公式 |
|---|
| 圓錐的側面積=母線的平方×π×(360分之扇形的度數) |
| 圓錐的側面積=1/2×母線長×底面周長 |
| 圓錐的側面積=π×底面圓的半徑×母線 |
| 圓錐的表面積=底面積+側面積 S=πr²+πrl (注l=母線) |
| 圓錐的體積=1/3底面積乘高 或 1/3πr^2h |
