時間序列預測法
時間序列預測法
時間序列預測法是一種歷史資料延伸預測,也稱歷史引伸預測法。是以時間數列所能反映的社會經濟現象的發展過程和規律性,進行引伸外推,預測其發展趨勢的方法。根據對資料分析方法的不同,又可分為:簡單序時平均數法、加權序時平均數法、移動平均法、加權移動平均法、趨勢預測法、指數平滑法、季節性趨勢預測法等。即把若干歷史時期的統計數值作為觀察值,求出算術平均數作為下期預測值。這種方法基於下列假設:“過去這樣,今後也將這樣”,把近期和遠期數據等同化和平均化,因此只能適用於事物變化不大的趨勢預測。
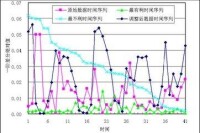
時間序列預測法
所反映出來的發展過程、方向和趨勢,進行類推或延伸,藉以預測下一段時間或以後若干年內可能達到的水平。其內容包括:收集與整理某種社會現象的歷史資料;對這些資料進行檢查鑒別,排成數列;分析時間數列,從中尋找該社會現象隨時間變化而變化的規律,得出一定的模式;以此模式去預測該社會現象將來的情況。
收集歷史資料,加以整理,編成時間序列,並根據時間序列繪成 統計圖。時間序列分析通常是把各種可能發生作用的因素進行分類,傳統的分類方法是按各種因素的特點或影響效果分為四大類:(1) 長期趨勢;(2)季節變動;(3)循環變動;(4)不規則變動。
分析時間序列。時間序列中的每一時期的數值都是由許許多多不同的因素同時發生作用后的綜合結果。
求時間序列的長期趨勢(T)季節變動(s)和不規則變動(I)的值,並選定近似的 數學模式來代表它們。對於數學模式中的諸未知參數,使用合適的技術方法求出其值。
利用時間序列資料求出長期趨勢、季節變動和不規則變動的數學模型后,就可以利用它來預測未來的長期趨勢值T和季節變動值s,在可能的情況下預測不規則變動值I。然後用以下模式計算出未來的時間序列的預測值Y:
加法模式T+S+I=Y
乘法模式T×S×I=Y
如果不規則變動的預測值難以求得,就只求 長期趨勢和季節變動的預測值,以兩者相乘之積或相加之和為時間序列的預測值。如果經濟現象本身沒有季節變動或不需預測分季分月的資料,則長期趨勢的預測值就是時間序列的預測值,即T=Y。但要注意這個預測值只反映現象未來的發展趨勢,即使很準確的 趨勢線在按時間順序的觀察方面所起的作用,本質上也只是一個平均數的作用,實際值將圍繞著它上下波動。
時間序列預測法可用於短期、中期和長期預測。根據對資料分析方法的不同,又可分為:簡單序時平均數法、加權序時平均數法、移動平均法、加權移動平均法、趨勢預測法、指數平滑法、季節性趨勢預測法、市場壽命周期預測法等。
簡單序時平均數法也稱算術平均法。如果事物呈現某種上升或下降的趨勢,就不宜採用此法。加權序時平均數法就是把各個時期的歷史數據按近期和遠期影響程度進行加權,求出平均值,作為下期預測值。
簡單移動平均法就是相繼移動計算若干時期的算術平均數作為下期預測值。
加權移動平均法即將簡單移動平均數進行加權計算。在確定權數時,近期觀察值的權數應該大些,遠期觀察值的權數應該小些。
上述幾種方法雖然簡便,能迅速求出預測值,但由於沒有考慮整個社會經濟發展的新動向和其他因素的影響,所以準確性較差。應根據新的情況,對預測結果作必要的修正。
指數平滑法即根據歷史資料的上期實際數和預測值,用指數加權的辦法進行預測。此法實質是由內加權移動平均法演變而來的一種方法,優點是只要有上期實際數和上期預測值,就可計算下期的預測值,這樣可以節省很多數據和處理數據的時間,減少數據的存儲量,方法簡便。是國外廣泛使用的一種短期預測方法。
季節趨勢預測法根據經濟事物每年重複出現的周期性季節變動指數,預測其季節性變動趨勢。推算季節性指數可採用不同的方法,常用的方法有季(月)別平均法和移動平均法兩種:a.季(月)別平均法。就是把各年度的數值分季(或月)加以平均,除以各年季(或月)的總平均數,得出各季(月)指數。這種方法可以用來分析生產、銷售、原材料儲備、預計資金周轉需要量等方面的經濟事物的季節性變動;b.移動平均法。即應用移動平均數計算比例求典型季節指數。
市場壽命周期預測法 就是對產品市場壽命周期的分析研究。例如對處於成長期的產品預測其銷售量,最常用的一種方法就是根據統計資料,按時間序列畫成曲線圖,再將曲線外延,即得到未來銷售發展趨勢。最簡單的外延方法是直線外延法,適用於對耐用消費品的預測。這種方法簡單、直觀、易於掌握。
某一城市從1984年到1994年中,每年參加體育鍛煉的人口數,排列起來,共有11個數據構成一個時間序列。我們希望用某個數學模型,根據這11個歷史數據,來預測1995年或以後若干年中每年的體育鍛煉人數是多少,以便於該城市領導人制訂一個有關體育健身的發展戰略或整個工作計劃。不同的時間序列有不同的特徵,例如一個人在一年中每天消耗的糧食基本上是相同的,把這365個數字排列起來。發現它所構成的時間序列總保持在一定水平,上下相差不太大,我們稱它是"平穩"時間序列。它的取值和具體是哪個時期無關,只和時期的長短有關。一般來說.只有屬於平穩過程的時間序列.才是可以被預測的。
年份 農業總產值 年份 農業總產值 年份 農業總產值
1980 220.553 1987 345.560 1994 483.960
1981 236.285 1988 357.909 1995 549.807
1982 267.120 1989 357.788 1996 600.986
1983 278.787 1990 357.671 1997 620.281
1984 312.089 1991 305.855 1998 667.542
1985 331.172 1992 362.848 1999 711.741
1986 338.848 1993 414.892
表1是揚州市1980~1999年農業總產值的有關數據資料,資料摘自《揚州統計年鑒2000》 ,表中產值按1990年不變價格計算。根據表1時間序列的資料,畫出時間序列折線圖1。通過觀察時間序列圖,可以看出此時間序列具有明顯的趨勢變動。在1980~1999年20年間,揚州市農業總產值總體呈明顯的上升趨勢。農業總產值的變化分為兩個時間段:1980~1990年時間序列呈曲線變化趨勢,1991~1999年時間序列呈線性變化趨勢。根據直觀的判斷,對時間序列採取分段處理的方法,即對1980~1990年的時間序列擬合二次曲線趨勢模型,對1991~1999年的時間序列擬合線性趨勢模型。
圖1農業總產值折線圖
(1)二次曲線趨勢模型:Yt=a+bt+ct^
上述方程中的三個未知參數a、b、c根據最小二乘法求得。即對時間序列擬合一條趨勢曲線,使之滿足下列條件:各實際值Yt與趨勢值〖AKY^〗t的離差平方和為最小,即∑(Yt-〖AKY^〗t)2=最小值,得到標準求解方程:
∑Y=na+b∑t+c∑t^2
∑tY=a∑t+b∑t^2+c∑t^3
∑t^2Y=a∑t^2+b∑t^3+c∑t^4
當取時間序列的中間時期數為原點時,有∑t=0,上式可簡化為:
∑Y=na+c∑t^2
∑tY=b∑t^2
∑t^2Y=a∑t^2+c∑t^4
經過計算,得到對揚州市1980~1990年農業總產值時間序列擬合的二次曲線模型為:
Y^t=316488.1+14584.3t-705.3t^2。
(2)線性趨勢模型:Y^t=a+bt
上述方程中的兩個未知參數a、b也是根據最小二乘法的原理求得。
b=n∑tY-∑t∑Y/n∑t^2-(∑t)^2
a=1/n(∑Y-b∑t)
同樣,為計算方便,取時間序列的中間時期數為原點,此時有∑t=0,上式可簡化為:
a=1/n∑Y
b=∑tY/∑t^2
經過計算,得到對揚州市1991~1999年農業總產值時間序列擬合的線性模型為:
Y^t=524212+51090.5t