擬序
擬序
擬序（quasi-order）是一種特殊的二元關係，它是集合上具有自反性及可傳遞性的二元關係。如a為一固定複數，對於任意複數x，y，有xR1y當且僅當|x-a|≥|y-a|。又如對於有向圖G的任意兩個節點u，v，有uR2v當且僅當u=v或者從u出發有一條有向路能夠連結u與v。集合X連同擬序R組成的二元組(X，R)稱為擬序集。
擬序
擬序
擬序
設R是集合A上的一個關係，如果R是反自反的和傳遞的，則稱R是A上的一個 擬序關係。一般用符號“ ”表示擬序關係。若 可記作，讀作“a小於b”。
例1 實數集上的小於關係R是擬序關係。
證明：對任何一個實數x都不存在x
對於任何實數x，y，如果x
對於任何實數x，y，z，如果x
例3 證明集合A的冪集P(A)上的關係“ ”是擬序關係。
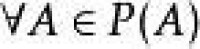
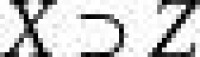
故 是P(A)上的擬序關係。
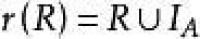(1) 如果R是一個擬序關係，則 是一個偏序關係；
(2) 如果R是一個偏序關係，則 是一個擬序關係。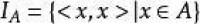
其中。根據定義很容易得到定理的證明。
例2 整數集Z上的“<”(小於關係)是擬序關係。
擬序
擬序
擬序
證明: (1)對，有X不真包含X，所以 具有反自反性。
擬序
擬序
擬序
(2)設X，Y，Z∈P(A)，若，則有，因此 具有傳遞性。
擬序
對於擬序有下面的定理。
集合X上的關係R是擬序的，則其必是反對稱的。
證明：用反證法。設R不是反對稱的，則必至少存在兩個元素a，b∈X，它們有∈R且∈R，由於R是擬序的，故它是傳遞的，由此必有∈R，但R又是反自反的，故矛盾。由此定理得證。
由此定理可知，擬序關係實際上是滿足反自反、反對稱且傳遞的關係，並且可以看出擬序關係與偏序關係有一定的聯繫——偏序是擬序的擴充，而擬序是偏序的縮減。
由擬序關係、偏序關係以及閉包的定義可知，擬序關係的自反閉包是一個偏序關係，由此可得下面的定理。
設R是集合上的關係，則：
擬序
擬序
擬序
基本信息
- 外文名
- quasi-order
目錄