切線法是通過曲線上的一些特徵點的切線的交點坐標關係來計算磁性體的產狀。
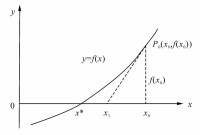
切線法
切線法又稱為
牛頓法,是一種一般情況下具有二階收斂速度的
非線性方程的數值解法。具體方法如下:
設是方程的根,又為附近的一個值,將在附近做
泰勒展開:
其中ξ在x和之間
令,則:
去掉的二次項得到:
即
令
並由此構成一個遞推式([]表示下標)
可以證明,當且滿足以下條件時,由以上遞推式產生的序列最後收斂到在上的唯一根
(1)
(2)
(3)上恆正或恆負
(4)初值應滿足
1.求解的實根
,由迭代公式有:
取得到:
所以
2.任意數開n次方
為了說明的方便,在此就常見的開3次方作較詳細的說明,對於其他的可以類比計算
設則
所以
採用遞推公式([]表示下標)即可求出的任意精度近似值。初值一般取與接近的整數.
舉例求,取,迭代結果如下:
從上面可以看出,只要迭代4次即可求出15位精度的近似值