立體角
物體對特定點三維空間的角度
立體角是以圓錐體的頂點為球心,半徑為1的球面被錐面所截得的面積來度量的,度量單位稱為“立體弧度”。和平面角的定義類似。在平面上我們定義一段弧微分s與其矢量半徑r的比值為其對應的圓心角記作dθ=ds/r;所以整個圓周對應的圓心角就是2n;與此類似,定義立體角為曲面上面積微元ds與其矢量半徑的二次方的比值為此面微元對應的立體角記作dΩ=ds/r^2;由此可得,閉合球面的立體角都是4n。錐體的立體角為,以錐體的定點為球心作球面,該錐體在球表面截取的面積與球半徑平方之比。單位為球面度。
角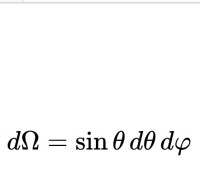 以觀測點為球心,構造一個單位球面;任意物體投影到該單位球面上的投影面積,即為該物體相對於該觀測點的立體角。
以觀測點為球心,構造一個單位球面;任意物體投影到該單位球面上的投影面積,即為該物體相對於該觀測點的立體角。
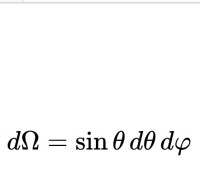
立體角
,角單球塊積,“平面角是單位圓上的一段弧長”類似。
式
在球坐標系中,自由球面的極小面積為: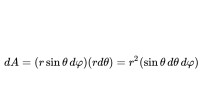 因此,極小立體角(單位球面上的極小面積)為:
因此,極小立體角(單位球面上的極小面積)為: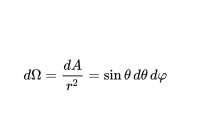 所以,立體角是投影面積與球半徑平方值的比,這和“平面角是圓的弧長與半徑的比”類似。對極小立體角做曲面積分即可得立體角:
所以,立體角是投影面積與球半徑平方值的比,這和“平面角是圓的弧長與半徑的比”類似。對極小立體角做曲面積分即可得立體角:
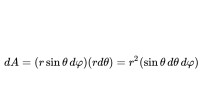
立體角
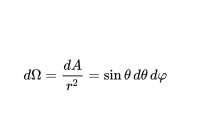
立體角
任意定向曲面相對於某一個點 P 的立體角,即為該曲面投影到以 P為球心的單位球面上的面積。令 為該單位球面上以P 為原點的極小面積的位置向量,可以得到以下公式: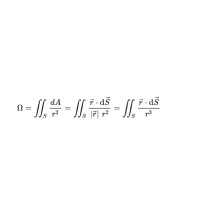
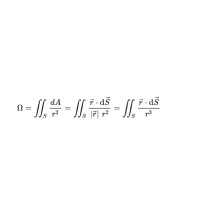
立體角
立體角的國際制單位是球面度(steradian,sr)。立體角有一個非國際制單位平方度,1sr= (180/π)square degree。
一個完整的球面對於球內任意一點的立體角為4πsr(對於球外任意一點的立體角為0sr):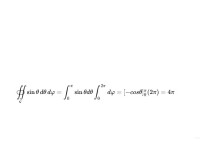
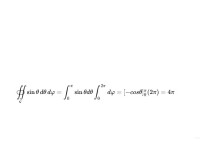
立體角
這個定理對所有封閉曲面皆成立,它也是高斯定律的主要依據。
頂角為2的圓錐的立體角為一個單位球的球冠。
(上面結果由下式得到)

立體角
應該注意阿基米德在2200年前不用微積分證明了球冠的表面積與半徑為球冠邊沿到球冠最低點的距離的圓的面積相等。球冠邊沿到球冠最低點的距離為
顯然,在單位圓中球冠立體角為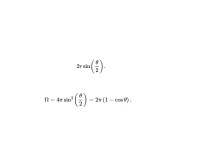
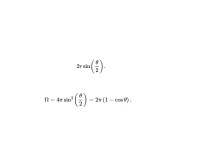
立體角
當立體角涵蓋整個球體,球冠變為有著立體角 4π的球,我們將4π稱為全方位立體角。當球冠變為有著立體角 2π的半球。
對於任意一個四面體OABC,其中O,A,B,C分別為四面體的四個頂點。下面給出一個公式,計算從O點觀察三角形ABC的立體角Ω的方便簡單的公式。令(均為各自平面內兩條直線的夾角,可以採用平面三角形的餘弦公式計算求得),

立體角
立體角在物理上有相當多的應用:
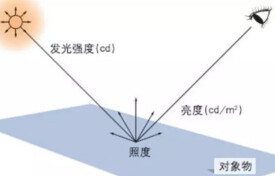
● 計算發光強度。
● 計算輻亮度(radiance),目的是為了衡量面輻射源的各向異性。
定義:垂直於給定方向上單位面積、單位時間、在單位立體角中放出的輻射能量
計算的公式:其中A 代表面積,Ω 代表立體角,λ 代表光的波長,Φ代表輻射通量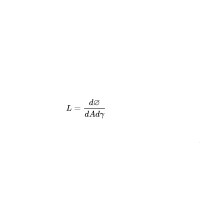
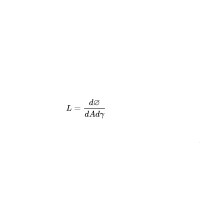
立體角