莫比烏斯函數
莫比烏斯提出的數論函數
莫比烏斯函數,數論函數,由德國數學家和天文學家莫比烏斯(August Ferdinand Möbius ,1790–1868)提出。梅滕斯(Mertens)首先使用μ(n)作為莫比烏斯函數的記號。而據說,高斯(Gauss)比莫比烏斯早三十年就曾考慮過這個函數。莫比烏斯函數在數論中有著廣泛應用。
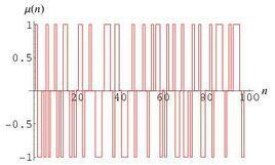
莫比烏斯函數(Möbius function)是指以下的函數:
在這裡,λ( n)是劉維爾函數
莫比烏斯函數是一個數論函數,它同時也是一個積性函數(i.e., a,b互質)
當n不等於1時,n所有因子的莫比烏斯函數值的和為0,
莫比烏斯函數完整定義的通俗表達:
1)莫比烏斯函數μ(n)的定義域是N
2)
3)當n存在平方因子時,
4)當n是素數或奇數個不同素數之積時,
5)當n是偶數個不同素數之積時,

莫比烏斯函數
莫比烏斯函數的求和函數,被稱為梅滕斯函數。
莫比烏斯函數有多個生成函數,其中一個與黎曼的ζ(s)有關
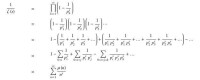
莫比烏斯函數
莫比烏斯函數的另一個生成函數如下
其中
以下是關於莫比烏斯函數的一些無窮級數: