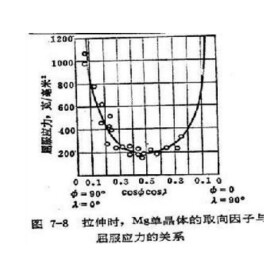
臨界應力

材料在力的作用下將發生變形。通常把滿足虎克定律規定的區域稱彈性變形區。把不滿足虎克定律和過程不可逆的區域稱塑性變形區。由彈性變形區進入塑性變形區稱之為屈服。其轉折點稱為屈服點。該點處的應力稱為屈服應力或臨界應力。

有些材料的屈服現象並不明顯，為了便於比較，就人為規定應力—應變偏離直線關係達某值(例如，通常規定為0.2%的永久變形)時的點為屈服點，該處的應力為臨界應力。

應該指出，塑料材料的臨界應力和載入速度，工作溫度等有非常明顯的依賴關係。

1、確定壓桿的臨界力是計算穩定問題的關鍵，臨界力既不是外力，也不是內力。它是壓桿在一定條件下所具有的反映它承載能力的一個標誌。不同的壓桿具有不同的臨界力，它的大小與壓桿的長度、截面的形狀和尺寸、兩端的支承情況以及材料的性質有關。

細長桿（λ≥λ）的臨界力計算式——歐拉公式

長度係數μ：兩端固定 μ=0.5

一端固定，另一端鉸支： μ=0.7

兩端鉸支： μ=1

一端固定，另一端自由： μ=2

2、歐拉公式的適用範圍：只有臨界應力不超過材料的比例極限時，用歐拉公式求得的臨界力和臨界應力才是正確的，即：

中長桿（l< l < l）的臨界應力計算式——直線公式

粗短桿（l≤l）的臨界應力計算式——強度計算式

3、臨界力計算的一般步驟

①確定長度係數μ（若壓桿兩端的支承情況在四周相同，則μ值相同。若壓桿的支承在兩個形心主慣性平面內的約束條件不同，則應分別選用相應的長度係數μ（μ或μ）的值。）

②計算柔度l（根據壓桿的實際尺寸，及兩端的約束情況，分別計算出在兩個形心主慣性平面內的柔度，從而得到l。）

③確定臨界力的計算式（根據最大的柔度λ，確定壓桿的類型及臨界力的計算公式。）

壓桿在臨界力的作用下，橫截面上的平均正應力稱為壓桿的臨界應力。柔度入是一個無量綱的量，它綜合反映了兩端支承情況、壓桿長度、截面形狀和尺寸等因素對臨界應力的影響。顯然，入越大，表示壓桿越細長，臨界應力就越小，臨界力也越小，壓桿越易失穩。反之，從越小，表示壓桿越粗短，臨界應力就越大，臨界力也越大，壓桿越不易失穩。所以，柔度入是壓桿穩定計算中一個重要的物理量。