屈服應力

應力去除時能產生永久變形的最小應力值可作為屈服應力的簡單定義。雖說這個定義對金屬材料是適用的，但在高聚物的場合就不同了，因為此時彈性可逆形變與塑性不可逆形變之間的差別變得不那麼明顯了。在高聚物的多種場合，例如拉伸試驗，屈服現象與由荷重-伸長曲線中觀察到的負荷極大值是一回事。因此，對高聚物的屈服應力還可定義為荷重-伸長曲線中負荷極大值時的真應力。由於該應力值在樣品伸長較小時即可達到，因此人們通常使用屈服應力的工程定義，即負荷極大值除以起始截面積。

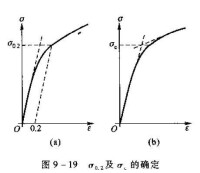
在某些情形下觀察不到荷重-伸長曲線中的負荷降，這就需要再給出屈服應力的其他定義。有一種定義是取荷重-伸長曲線轉折處兩側的切線，其交點所對應的應力值作為屈服應力。另外一種方法是取應力一應變曲線的起始部分的斜率，然後偏移一個應變數，例如0.2%，再按此斜率作一平行線，它與應力一應變曲線的交點定義的應力值，叫做偏移應力或檢驗應力，可以此定為屈服應力。

此外，屈服應力還描述為：材料在單向拉伸（或壓縮）過程中，由於加工硬化，塑性流動所需的應力值隨變形量增大而增大。對應於變形過程某一瞬時進行塑性流動所需的真實應力叫做該瞬時的屈服應力，亦稱流動應力。如果忽略材料的加工硬化，可以認為屈服應力為一常數，並近似等於屈服極限（σ）。實際上，屈服應力是一個由形變速度、形變溫度、形變程度決定的函數，且這些參數彼此相互影響，並通常與材料特性相關。

在金屬的彈性變形達到極限后，其強度就會發生小範圍的波動，這時也就是塑性變形開始了。這個點即是屈服點，這時所受的應力就叫做屈服應力或屈服強度。屈服點之前一般金屬的變形量與拉力接近一次線性關係，屈服點之後就變為二次線性關係（拋物線），即拉力增加不大，但產生的變形量卻相對較大。

對於多晶體材料而言，材料塑性變形的屈服應力一般取殘餘應變為0.2%時所加的應力，即所謂的σ，如圖（a）所示。另一種方法是把應力-應變曲線的彈性階段及塑性階段曲線外推的交點作為屈服應力，如圖（b）所示。

有些鋼材（如高碳鋼）無明顯的屈服現象，通常以發生微量的塑性變形（0.2%）時的應力作為該鋼材的屈服強度，稱為條件屈服強度。

屈服應力是一個應力界限，應力低於它時材料具固體特性，不會流動，應力高於屈服應力時，開始流動併產生無限的形變，顯示牛頓粘性。

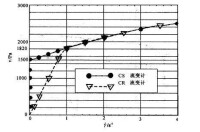
用控制應力（CS）型流變儀測量屈服應力最理想，用這種類型的流變儀測量時，向轉子施加受控應力，當應力小於樣品的屈服應力時，轉子被樣品“夾住”不能動，因為轉子不能動，儀器便測不到有效的剪切速率，流動曲線與應力軸完全重疊，一旦應力超過屈服值，轉子開始轉動，應力隨剪切速率而增加，流動曲線以一定斜率上升，如下圖中的圓點曲線，屈服應力可精確得到。

如果用控制速率（CR）型流變儀，這種儀器的馬達接了測速發電機，使馬達以設定的轉速旋轉並驅動轉子，馬達開始緩慢旋轉，其轉速由測速發電機的電信號檢測，在達到屈服應力前，雖然轉子被樣品“夾住”不能動，扭矩彈簧略卻會微偏轉（偏轉的程度與彈簧的軟硬程度有關），因此這段的流動曲線不是沿應力軸上升，而是一條偏離應力軸的直線，

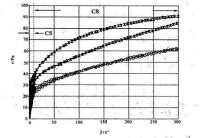
如上圖中的三角點曲線，它只是來自測速發電機及扭矩彈簧的信號，而不是樣品的流變曲線。當剪切樣品的應力隨剪切速率而增加並達到屈服應力時，轉子才開始旋轉（從靜止狀態立即加速到馬達的轉速），流動曲線的斜率急劇改變，轉子轉速與馬達轉速同步增長。用CR型流變儀測量屈服阻力時，將流動曲線斜率發生突變點的剪切應力值定義為樣品的屈服應力，這樣測得的屈服值通常要比用CS模式測得的值略大些。因此用帶有軟彈簧扭矩感測器的CR型流變儀測量屈服應力，尤其是低屈服值的樣品的測量結果是會受到質疑的。下圖中的三角點曲線是用帶有全量程扭轉為90°的軟彈簧的CR型流變儀測得的。現在有些CR型流變儀的扭矩彈簧已用硬彈簧，如HAAKE的RTl0流變儀用的硬彈簧的扭矩全量程僅扭轉0.5°，大大提高了測量屈服應力韻可靠性。

上圖是用HAAKE的RSl00犁流變儀試驗的兩種西紅柿醬的流動曲線涮試驗用兩種模式（CS與CR）組合運行，小於屈服應力用CS模式，以後用CR模式。可以看出在屈服應力前的“流動曲線”仍然略偏離應力軸，這種現象被解釋為在屈服應力前樣品有某種程度的蠕變，也許還發生一些彈性形變。

有Hall-Petch公式可見，屈服應力既受晶內的成分、組織的影響，又受晶粒尺寸、晶界組織的影響。所以，與彈性模量不同，它是一個內部因素即成分、組織敏感的力學性能；另一方面，它又與諸多外部因素如溫度、變形速度和應力狀態等有密切關係，而且這些關係都是材料力學性能分析和試驗研究中經常要注意到的問題，所以，以下主要討論這些外部因素對屈服應力的影響。

溫度升高，屈服應力下降。通常有兩方面的原因：其一是隨溫度上升，原子熱振動增大，點陣間距增加，彈性模量下降，晶格對位錯運動的阻力也下降。不過，不同基體的晶體結構對溫度的敏感性不同，三種常見結構的單晶體的臨界分切應力與溫度的關係是，體心立方結構最敏感，密排六方次之之，面心立方最不暾感。其二是溫度上升，阻礙位錯運動的因素可借熱激活和原子擴散等過程得到克服。

凡和原子擴散有關的位錯運動阻力必然要受到變形速度的影響。一般說來，變形速度上升相當於溫度下降，通過測試普通碳鋼的屈服應力與載入速度的關係。可得在載入速度≈10N/mm/s附近時大致相當於得到最低和穩定的屈服應力值。所以，為了測得可比的屈服應力，標準試驗方法中通常規定的載入速度應<30N/mm/s。

同一材料在不同載入方式下，有著不同的屈服應力。這是因為，從實質上看只有切應力才引起材料的塑性變形，而不同的應力狀態下，材料中一點所受到的切應力分量和正應力分量的比值不同，即軟性係數α不同。α愈大即切應力相對愈大的應力狀態下，其有效屈服強度就愈低，反之愈高。所以，按不同載入方式如扭轉，拉伸，彎曲，三向不等拉伸所得到的有效屈服強度一個比一個高。

在塑性變形階段，實際應力曲線上每一點的應力值，都可理解為材料在相應的變形程度下的屈服點。

如果卸載后反向載入，由拉伸改為壓縮，應力與應變的關係又會產生什麼樣的變化呢？試驗表明，反向載入時，材料的屈服應力較拉伸時的屈服應力有所降低，出現所謂反載軟化現象。反向載入時屈服應力的降低量，視材料的種類及正向載入的變形程度不同而異。關於反載軟化現象，有人認為可能是因為正向載入時材料中的殘餘應力引起的。

結構屈服應力的求法，一般借用前期固結壓力求結構屈服應力，其主要方法有:Casagrande法和Schmertman法等方法。