勒讓德函數
勒讓德函數
在數學中,勒讓德函數Pλ,Qλ和相關的勒讓德函數Pλ,Qλ是勒讓德多項式與非整數度的泛化。
在數學中,勒讓德函數和相關的勒讓德函數 是勒讓德多項式與非整數度的泛化。
相關的勒讓德函數是勒讓德方程的解
其中複數λ和μ分別稱為相關的勒讓德函數的度數和順序。勒讓德多項式是階數的勒讓德函數。
這是一個具有三個常規奇異點的二階線性方程。像所有這樣的等式,它可以通過變數的變化被轉換為超幾何微分方程,並且其解可以用超幾何函數來表示。
這些功能實際上可以用於一般複雜參數和參數:
分母中包含伽馬函數,是超幾何函數。
二階微分方程具有第二個解,其定義為。
勒讓德P和Q函數之間有用的關係是Whipple的公式。
勒讓德函數可以寫成輪廓積分。例如,
其中輪廓沿正方向繞著點1和z旋轉,並且不繞-1。對於真正的x,我們有
的真實積分表示在其中 是的雙陪集空間(見區域球面 功能)。實際上,上的傅里葉變換由
其中,
勒讓德多項式是下列勒讓德微分方程的多項式解:
其中n 為正整數。
勒讓德多項式的生產函數為
前幾個勒讓德多項式:
勒讓德多項式在取決滿足如下的正交關係式:
其中F為超幾何函數,v非整數。如v為整數,則解為勒讓德多項式
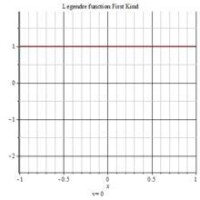
第一類勒讓德函數2D圖
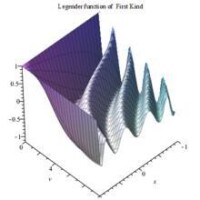
第一類勒讓德函數3D圖
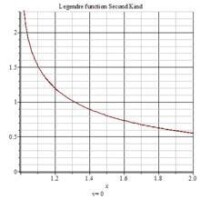
第二類勒讓德函數2D圖
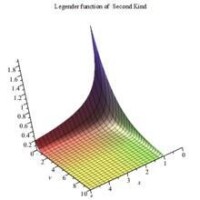
第二類勒讓德函數3D 圖
