一筆畫問題
用於幾何畫圖領域的圖論
傳統意義上的幾何學是研究圖形的形狀大小等性質,而存在一些幾何問題,它們所研究的對象與圖形的形狀和線段的長短沒關係,而只和線段的數目和它們之間的連接關係有關,比如一筆畫問題就是如此。即平面上由曲線段構成的一個圖形能不能一筆畫成,使得在每條線段上都不重複。例如漢字“日”和“中”字都可一筆畫,而“田”和“目”則不能。兩兩相連區域可一筆畫,例如,平面4個區域兩兩相連區域可一筆劃;輪胎狀上7個兩兩相連區域可一筆畫;我們可以構造一個多維空間的無窮個兩兩相連區域一筆劃。
眾所周知的“哥尼斯堡城‘七橋問題’”被大數學家歐拉開創了數學新分支-----圖論。也就是“一筆畫”。一筆畫圖形的必要條件是:奇點數目是0或者2。圖⑴的“七橋問題”A,B,C,D都是奇節點,數目是4,所以不能夠“一筆畫”。我們把節點轉換回來,成為“節面”(區域),來考慮“一筆畫”。
在平面中,4個或者4個以下的區域可以構成兩兩相連的區域,可以一筆畫。圖⑵。每個區域必須是單連通的,就是一個區域不能夠是分成2塊或者2塊以上。圖⑶就不是單連通的。這是著名的四色猜想。大家知道,平面上不可能有兩兩相同的5個區域。緊緻封閉平面,在一個輪胎狀的表面,7個或者7個以下的區域可以構成兩兩相連的區域。可以“一筆劃”。把圖(A)上下對摺以後,再左右對摺,形成一個輪胎狀,7個區域兩兩相連。
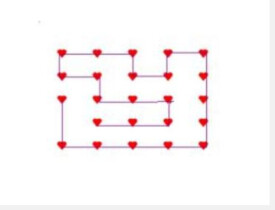
一筆畫問題
數學家歐拉找到一筆畫的規律是:
⒈凡是由偶點組成的連通圖,一定可以一筆畫成。畫時可以把任一偶點為起點,最後一定能以這個點為終點畫完此圖。
⒉凡是只有兩個奇點的連通圖(其餘都為偶點),一定可以一筆畫成。畫時必須把一個奇點為起點,另一個奇點終點。
⒊其他情況的圖都不能一筆畫出。(有偶數個奇點除以二便可算出此圖需幾筆畫成。)
比如附圖:(a)為⑴情況,因此可以一筆畫成;(b)(c)(d)則沒有符合以上兩種情況,所以不能一筆畫成。
◎頂點與指數:設一個平面圖形是由有限個點及有限條弧組成的,這些點稱為圖形的頂點,從任一頂點引出的該圖形的弧的條數,稱為這個頂點的指數。
◎奇頂點:指數為奇數的頂點。
◎偶頂點:指數為偶數的頂點
先定義能一筆畫出並回到起點的圖為歐拉圖,連通就是說任意兩個節點之間可以找到一條連接它們的線。這個要求看來很重要,直觀方法中與這一點對應的是說原圖本身不能是分成多個的。
設G為一歐拉圖,那麼G顯然是連通的。另一方面,由於G本身為一閉路徑,它每經過一個頂點一次,便給這一頂點增加度數2,因而各頂點的度均為該路徑經歷此頂點的次數的兩倍,從而均為偶數。反之,設G連通,且每個頂點的度均為偶數,欲證G為一歐拉圖。為此,對G的邊數歸納。當m=1時,G必定為單結點的環,顯然這時G為歐拉圖。設邊數少於m的連通圖,在頂點度均為偶數時必為歐拉圖,現考慮有m條邊的圖G。設想從G的任一點出發,沿著邊構畫,使筆不離開
而且不在構畫過的邊上重新構畫。由於每個頂點都是偶數度,筆在進入一個結點后總能離開那個結點,除非筆回到了起點。在筆回到起點時,它構畫出一條閉路徑,記為H。從圖G中刪去H的所有邊,所得圖記為G’,G’未必連通,但其各頂點的度數仍均為偶數.考慮G的各連通分支,由於它們都連通,頂點度數均為偶數,而邊數均小於m,因此據歸納假設,它們都是歐拉圖。此外,由於G連通,它們都與H共有一個或若干個公共頂點,因此,它們與H一起構成一個閉路徑。這就是說,G是一個歐拉圖。
1736年,歐拉證實:七橋問題的走法根本不存在。同時,他發表了“一筆畫定理”:一個圖形要能一筆畫完成必須符合兩個條件,即圖形是封閉聯通的和圖形中的奇點(與奇數條邊相連的點)個數為0或2。歐拉的研究開創了數學上的新分支――拓撲學的先聲。