EMD

經驗模態分解（Empirical Mode Decomposition，簡稱EMD）是依據數據自身的時間尺度特徵來進行信號分解，無須預先設定任何基函數。

這一點與建立在先驗性的諧波基函數和小波基函數上的傅里葉分解與小波分解方法具有本質性的差別。正是由於這樣的特點，EMD方法在理論上可以應用於任何類型的信號的分解，因而在處理非平穩及非線性數據上，具有非常明顯的優勢，適合於分析非線性、非平穩信號序列，具有很高的信噪比。所以，EMD方法一經提出后，就在不同的工程領域得到了迅速有效的應用，例如在海洋、大氣、天體觀測資料與地震記錄分析、機械故障診斷、密頻動力系統的阻尼識別以及大型土木工程結構的模態參數識別方面。該方法的關鍵是經驗模式分解，它能使複雜信號分解為有限個本徵模函數（Intrinsic Mode Function，簡稱IMF），所分解出來的各IMF分量包含了原信號的不同時間尺度的局部特徵信號。經驗模態分解法能使非平穩數據進行平穩化處理，再進行希爾伯特變換獲得時頻譜圖，得到有物理意義的頻率。與短時傅立葉變換、小波分解等方法相比，這種方法是直觀的、直接的、后驗的和自適應的，因為基函數是由數據本身所分解得到。由於分解是基於信號序列時間尺度的局部特性，因此具有自適應性。

經驗模態分解(EMD)方法的實質是通過特徵時間尺度來識別信號中所內含的所有振動模態(Intrinsic Oscillatory Mode)。在這一過程中，特徵時間尺度及IMF的定義都具有一定的經驗性和近似性。與其他信號處理方法相比，EMD方法是直觀的、間接的、后驗的、自適應的，其分解所用的特徵時間尺度是源自於原始信號的。

EMD分解方法是基於以下假設條件：

⑴數據至少有兩個極值，一個最大值和一個最小值；

⑵數據的局部時域特性是由極值點間的時間尺度唯一確定；

⑶如果數據沒有極值點但有拐點，則可以通過對數據微分一次或多次求得極值，然後再通過積分來獲得分解結果。這種方法的本質是通過數據的特徵時間尺度來獲得本徵波動模式，然後分解數據。這種分解過程可以形象地稱之為“篩選（sifting）”過程。

為了從原始信號中分解出內模函數，經驗模態分解方法，過程如下：

(1)找到信號x(t)所有的極值點；

(2)用3次樣條曲線擬合出上下極值點的包絡線emax(t)和emin(t)，並求出上下包絡線的平均值m(t)，在x(t)中減去它:h(t)=x(t)-m(t)；

(3)根據預設判據判斷h(t)是否為IMF；

(4)如果不是，則以h(t)代替x(t)，重複以上步驟直到h(t)滿足判據，則h(t)就是需要提取的IMFCK(t)；

(5)每得到一階IMF，就從原信號中扣除它，重複以上步驟;直到信號最後剩餘部分rn就只是單調序列或者常值序列。

這樣，經過EMD方法分解就將原始信號x(t)分解成一系列IMF以及剩餘部分的線性疊加：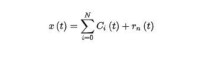

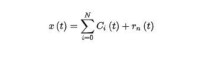
EMD方法擁有諸多優勢，主要表現在以下幾方面：

主成分分析根據

從EMD理論的介紹可以看出，EMD的目的是將組成原始信號的各尺度分量不斷從高頻到低頻進行提取，則分解得到的特徵模態函數順序是按頻率由高到低進行排列的，即首先得到最高頻的分量，然後是次高頻的，最終得到一個頻率接近為0的殘餘分量。而針對不斷進行分解的信號而言，能量大的高頻分量總是代表了原信號的主要特性，是最主要的組成分量，所以EMD方法是一種將信號的主要分量先提取出來，然後再提取其他低頻部分分量的一種新的主成分分析方法。

自適應時頻分析

EMD方法的基本思想是把信號分解成一組單分量信號IMF的組合，再對各分量進行希爾伯特變換，得到瞬時特徵量，並將這些瞬時特徵量變換到時一頻平面形成希爾伯特譜。實際上，EMD方法等價於定義了一組含有自適應分解特性的廣義基，從傳統基函數定義角度來看，EMD所定義的自適應廣義基在信號處理領域屬於對基函數的一種創新。這種基函數不是事先預定或強制給定的，而是依賴信號本身，只和信號本質特徵有關，能根據分解過程中信號的特徵而自適應發生改變，故EMD方法具有自適應時頻分析的特徵。

信號局瞬特性表徵

EMD方法的數學基礎和核心是希爾伯特變換，而希爾伯特變換的主要目的是得到單分量信號的瞬時頻率，強調信號的局部瞬時特性，徹底避免了傳統傅里葉變換利用已知頻率分量擬合原序列而產生虛假頻率諧波的現象。

EMD方法將信號分解成有限個IMF的單分量信號組合，定義了信號瞬時頻率的物理實體。與傳統時頻分析方法的頻率定義方式完全不同，利用相位導數求取頻率的經典定義方法，對信號不同頻率成分分量的瞬時頻率進行了精確的描述和表達。所以，EMD方法對時變非線性非平穩信號也具有很好的分析效果，具有有效的局瞬特性表徵能力。

端點效應處理

EMD是通過多次的篩選過程來逐個分解IMF，在每一次的篩選過程中，要根據信號的上、下包絡來計算信號的局部平均值；上、下包絡是由信號的局部極大值和極小值通過樣條插值演演算法給出。由於信號兩端不可能同時處於極大值和極小值，因此上、下包絡在數據序列的兩端不可避免地會出現發散現象。以左端點為例，如果該點為極大值點，那麼上包絡線可以把它作為左端終點，不會發生大幅度的擺動；對於下包絡線由於左端點不是極小值點，則無法確定它的左端終點，產生大幅度的擺動，給篩選過程引入誤差，並且這種發散的結果會隨著篩選過程的不斷進行，逐漸向內“污染”整個數據序列而使得所得結果嚴重失真。在EMD中，這種現象稱為端點效應，它會直接影響EMD的質量。

對有限長信號的分析或處理無可避免地要遇到端點問題，在小波變換、卷積濾波或傅里葉頻譜等使用卷積濾波的信號分析方法中，只需採用加窗或延拓信號等簡單措施就可解決端點問題，且其端點處理的影響最多波及到距端點一個窗寬的範圍內，而不會影響到對信號內部的分析結果。EMD同樣要面對這種問題的存在，且由於其分解需要確定端點處的局部均值，其端點問題相對其他信號分析方法而言要更複雜些，尤其對於低頻的IMF分量來說，這種端點效應所引起的誤差更加嚴重。因此，解決端點問題對於EMD以及其他信號處理方法，都具有理論和實際意義。

模態混疊問題

經驗模態分解作為一種非常靈活的自適應時頻數據分析方法，廣泛地應用於從非線性和非平穩過程的雜訊中提取特徵信號。但這種方法在實際應用中也會存在一些問題，如對時問尺度跳躍性變化的信號進行EMD時，會出現以下情況：不同時間尺度特徵成分被分解到一個特徵模態函數分量，或者同一時間尺度成分出現在不同的特徵模態函數中，稱這種現象為模態混疊，它的出現受原始信號頻率特徵的影響且和EMD的演演算法有關。一旦模態混疊產生，特徵模態函數就沒有任何物理意義，此時多個物理過程用一個特徵模態函數來表示，儘管最後的時頻分析能夠一定程度上緩解模態混疊，但是不可避免地“污染”後面特徵尺度的分解。Huang在文獻中指出：模態混疊產生的主要原因是信號的間斷性（不連續性）。模態混疊使得EMD結果在時頻分佈上產生嚴重的鋸齒線，並且使得一些特徵模態函數失去其物理意義，從而導致EMD的性能嚴重下降。為此，Huang通過在EMD操作前加入一個間斷測試，用於解決模態混疊問題。然而，此測試本身存在如下兩個問題。首先，測試基於一個主觀選擇的尺度，從而使得EMD不再完全自適應；其次，此間斷測試的前提條件是信號的尺度是清晰可分的（主觀可分的）。因此，如果人的肉眼無法找到一個主觀選擇的尺度，則模態混疊問題依然存在。