圓面積公式
一種定理定律
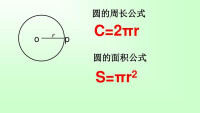
圓面徠積公式是一種定理定律。為圓周率*半徑的平方,用字母可以表示為:S=πr²或S=π*(d/2)²。(π表示圓周率(3.1415926……),r表示半徑,d表示直徑)。
圓的半徑:r
直徑:d
圓周率:π(數值為3.1415926至3.1415927之間……無限不循環小數),通常採用3.14作為π的數值

圓面積公式
圓面積: ;
圓面積=圓周率×半徑×半徑
半圓的面積:S=(πr)÷2
半圓的面積=圓周率×半徑×半徑÷2
圓環面積: S-S=π(R-r)(R為大圓半徑,r為小圓半徑)
圓環面積=外大圓面積-內小圓面積
圓面積公式
圓面積公式
圓的周長:或
圓的周長=直徑×圓周率
圓面積公式

圓面積公式
半圓的周長:或者
半圓周長=圓周率×半徑+直徑

開普勒
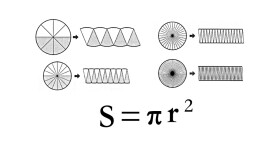
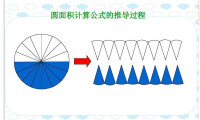
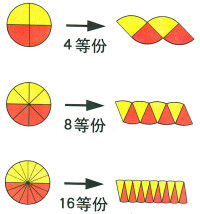
開普勒當過數學老師,他對求面積的問題非常感興趣,曾進行過深入的研究。他想,古代數學家用分割的方法去求圓面積,所得到的結果都是近似值。為了提高近似程度,他們不斷地增加分割的次數。但是,不管分割多少次,幾千幾萬次,只要是有限次,所求出來的總是圓面積的近似值。要想求出圓面積的精確值,必須分割無窮多次,把圓分成無窮多等分才行。
開普勒也仿照切西瓜的方法,把圓分割成許多小扇形;不同的是,他一開始就把圓分成無窮多個小扇形。圓面積等於無窮多個小扇形面積的和,所以 在最後一個式子中,各段小弧相加就是圓的周長2πR,所以有 這就是我們所熟悉的圓面積公式。
開普勒運用無窮分割法,求出了許多圖形的面積。1615年,他將自己創造的這種求圓面積的新方法,發表在《葡萄酒桶的立體幾何》一書中。
開普勒大膽地把圓分割成無窮多個小扇形,並果敢地斷言:無窮小的扇形面積,和它對應的無窮小的三角形面積相等。他在前人求圓面積的基礎上,向前邁出了重要的一步。
《葡徠萄酒桶的立體幾何》一書,很快在歐洲流傳開了。數學家們高度評價開普勒的工作,稱讚這本書是人們創造求圓面積和體積新方法的靈感源泉。
在半徑為R的圓中,因為360°的圓心角所對的扇形的面積就是圓面積S=πR;;,所以圓心角為n°的扇形面積:
S=(nπR)÷360
扇形還有另一個面積公式
S=1/2lR (其中l為弧長,R為半徑)
本來S=(nπR)÷360
按弧度制。2π=360度。因為n的單位為度。所以l為角度為n時所對應的弧長。即.l=θR=(n/180)π×R
∴s=(n/180)π*R*π*R/2π=1/2lR.
把圓平均分成若干份,可以拼成一個近似的長方形。長方形的寬就等於圓的半徑(r),長方形的長就是圓周長(C)的一半。長方形的面積是ab,那圓的面積就是:圓的半徑(r)乘以二分之一周長C,S=r*C/2=r*πr。
圓周長(C):圓的直徑(d),那圓的周長(C)除以圓的直徑(d)等於π,那利用乘法的意義,就等於 π乘以圓的直徑(d)等於圓的周長(C),C=πd。而同圓的直徑(d)是圓的半徑(r)的兩倍,所以就圓的周長(C)等於2乘以π乘以圓的半徑(r),C=2πr。